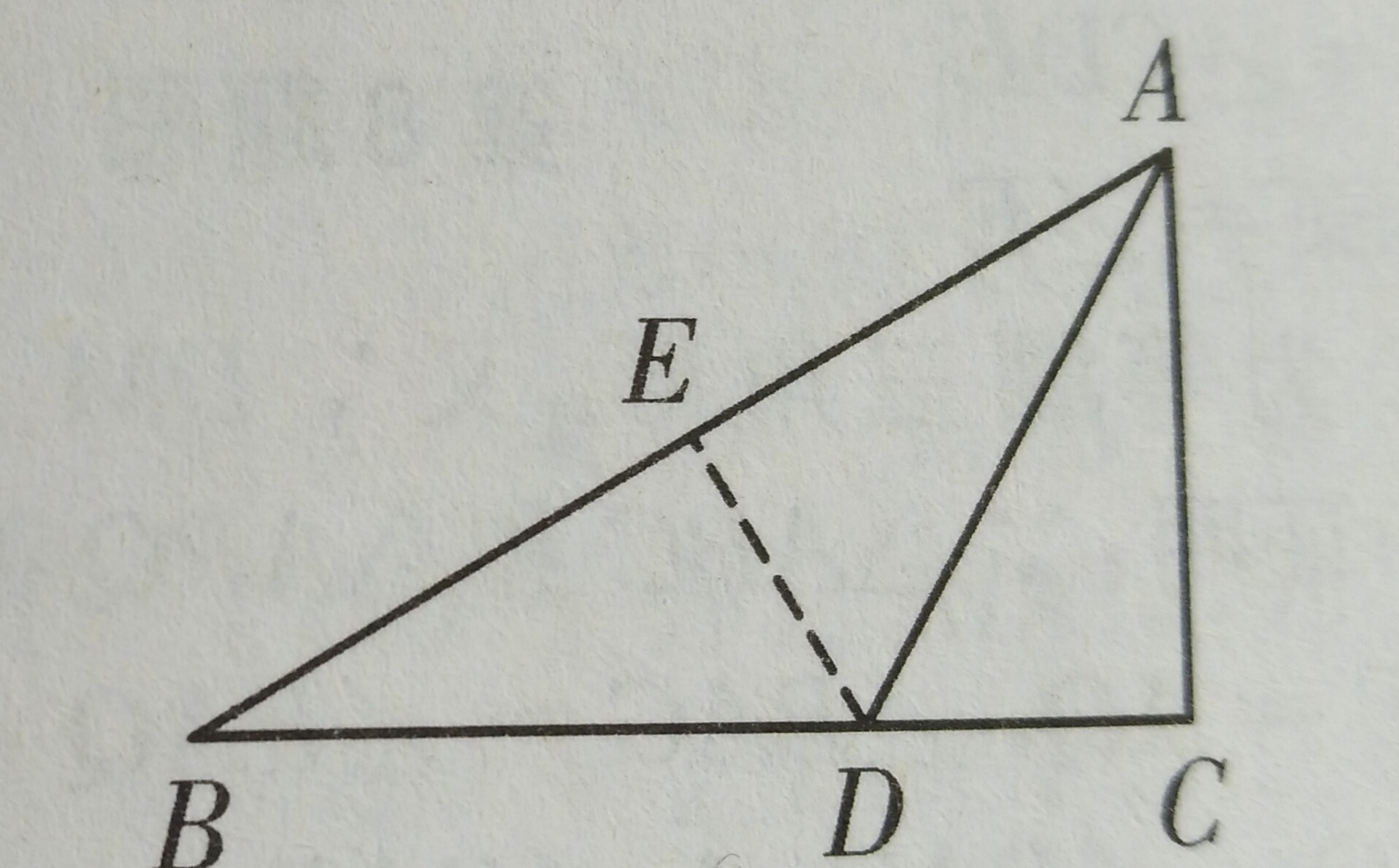
1、如图，在△ABC中，AD平分∠BAC，∠C=90°，DE⊥AB，垂足为E，点F在AC上，BD=FD。
(1)求证：CF=EB
(2)若AB=14，AF=8，求CF的长。

2、如图，∠C=90°，∠B=30°，AD是△ABC的角平分线。
(1)求证：BD=2CD
(2)若CD=2，求△ABD的面积。

3、如图所示，四边形ABDC中，∠D=∠B=90°，点O为BD的中点，且OA平分∠BAC。
(1)求证：OC平分∠ACD
(2)求证：OA⊥OC
(3)求证：AB+CD=AC

                                      
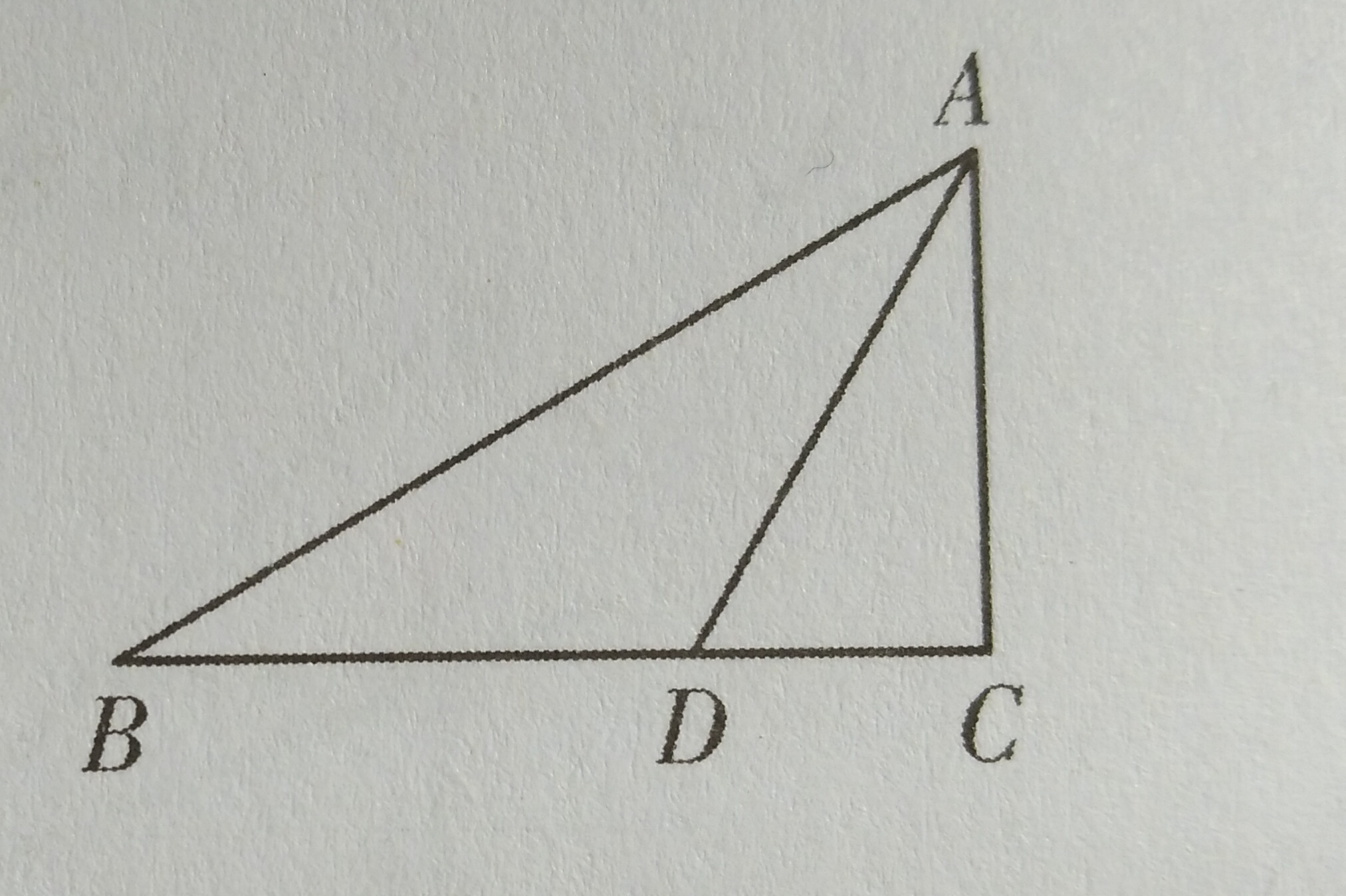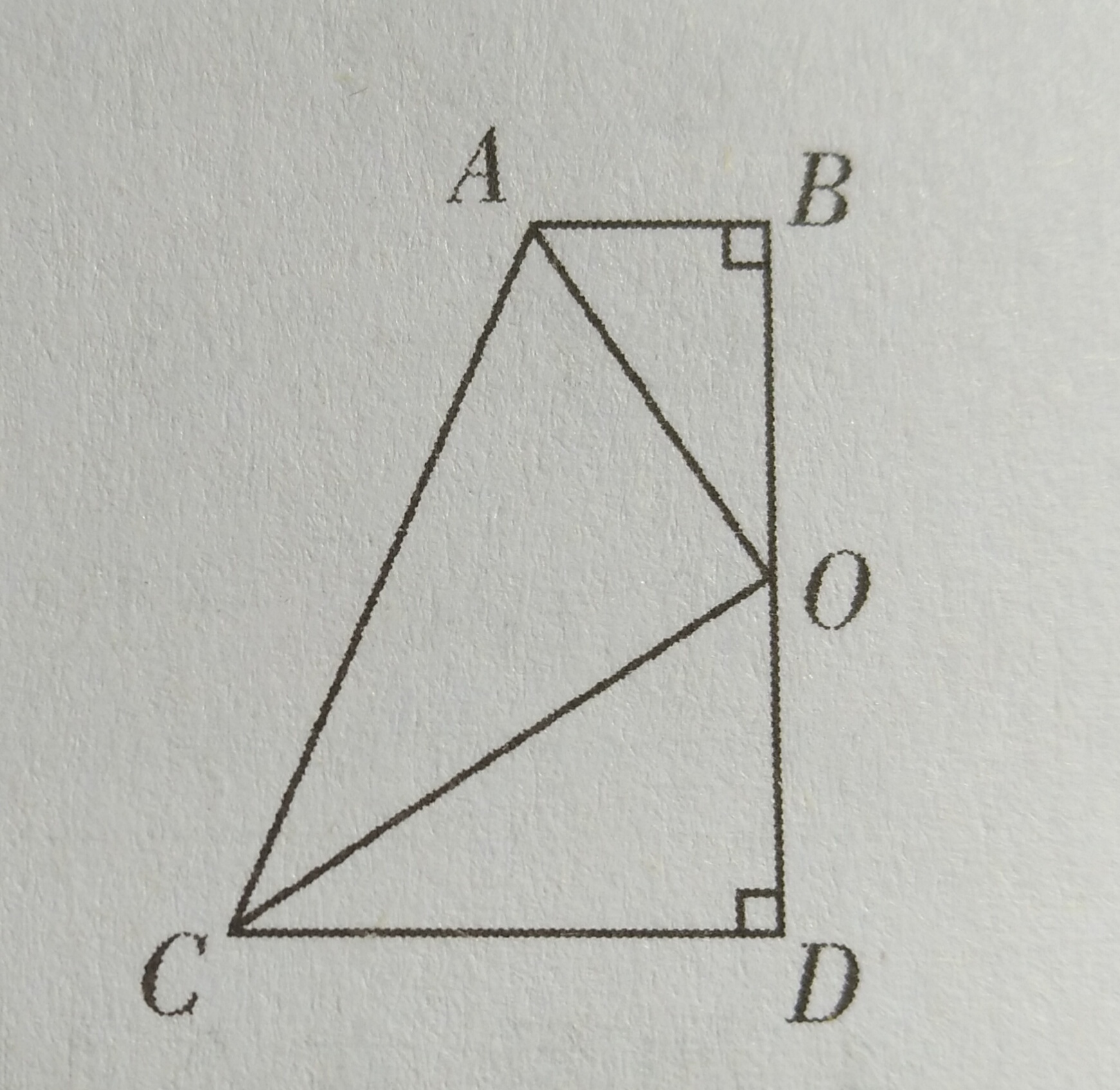
         第1题图                                   第2题图                                            第3题图
参考答案：
1、(1)∵AD是角平分线  ∠C、∠E=90°
          ∴CD=ED (角平分线上的点到角两边距离相等)
        又∵FD=BD (已知条件)
            ∴△FCD≌△BED (HL)
           ∴CF=EB
    (2) ∵AD是角平分线  ∠C、∠E=90°
          ∴△ACD≌△AED (AAS或已被公认)                      
           ∴AC=AE
        又 ∵FC=EB
             ∴ AC   +  FC=14
             即AF+FC+FC=14
         ⇨     8+ FC+FC=14
                              FC=3
2、(1)作DE⊥AB
       ∵AD是角平分线 ∠C=90°
       ∴ED=CD
       在△EBD中 ED=1/2BD(∠B=30°)
       ∴BD=2ED
        ∴BD=2CD(等量代换)

  (2)△EBD中
      BE²+ED²=BD²
  ⇨BE²+2²=4²
             BE=2√3
      AB=2√2×2=4√3
     S△ABD=底×高×1/2=4√3×2×1/2=4√3
3、(1)作OE⊥AC
        ∵OA是角平分线 ∠B、∠E=90°
        ∴OE=OB
    又∵OD=OB(中点已知)
        ∴OE=OD
        ∴CO也是角平分线

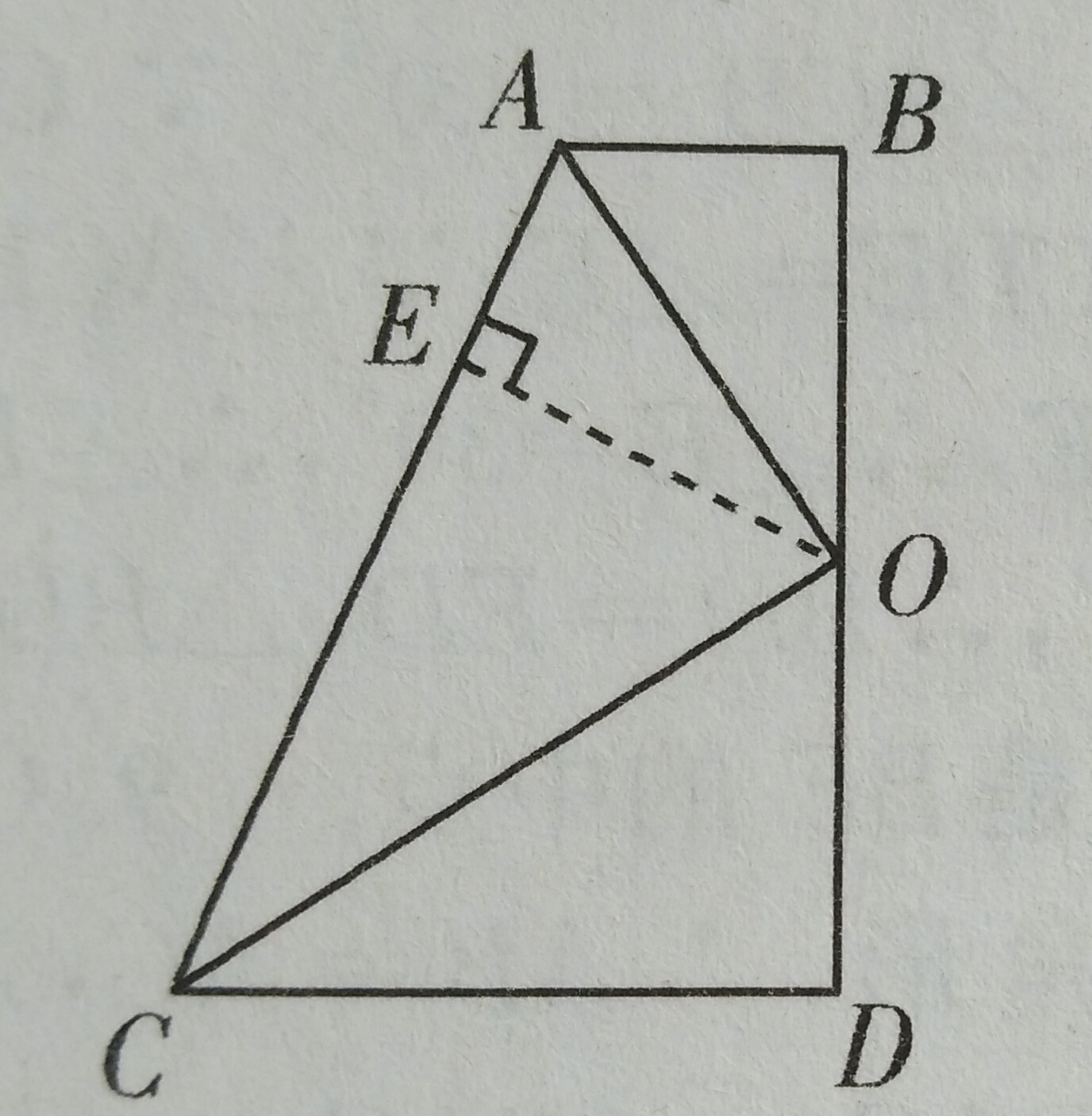
(2)方法一：角平分线法
    ∵EO=BO  AO=AC
    ∴△AEO≌△ABO(HL)
    ∴∠AOB=∠AOE
   同理△CEO和△CDO中
    ∠EOC=∠COD
    ∴∠AOE+∠EOC=180÷2=90°
        即OA⊥OC
方法二：平行线法
    ∵AB∥CD(∠B、∠D=90°)
    ∴∠A+∠C=180°(同旁互补)
 又∵∠A左=∠A右 ∠C上=∠C下
     ∴∠A左+∠C上=90°
     ∴∠AOC=90°
(3)∵△AEO≌△ABO
        △CEO≌△CDO (第2小题已证)
        ∴AE=AB
            CE=CD
       而 AE+CE=AC
       ∴AB+CD=AC

潜龙家教谭老师全程解题并录入，时间精力有限，错漏之处恳请您不吝指正，感谢！