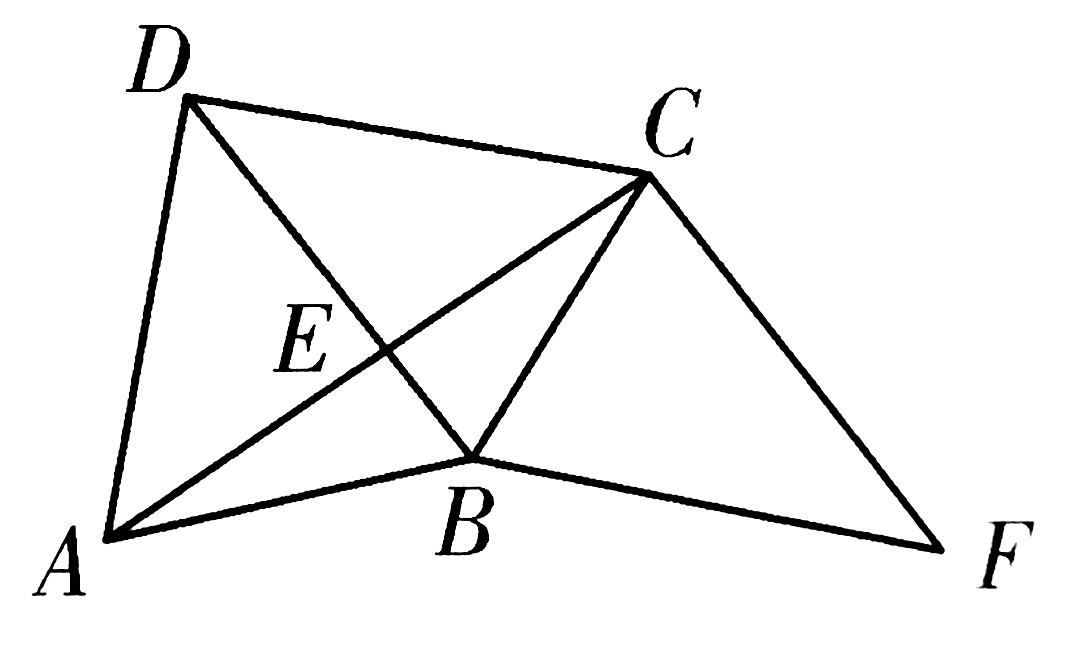
1、如图，四边形ABCD的对角线AC⊥BD，垂足为点E，AB=BC，点F为四边形ABCD外一点，且∠FCA=90°，∠CBF=∠DCB。
(1)求证：四边形DBFC是平行四边形
(2)如果BC平分∠DBF，∠F=45°，BD=2，求AC的长。
                                                                                                                  
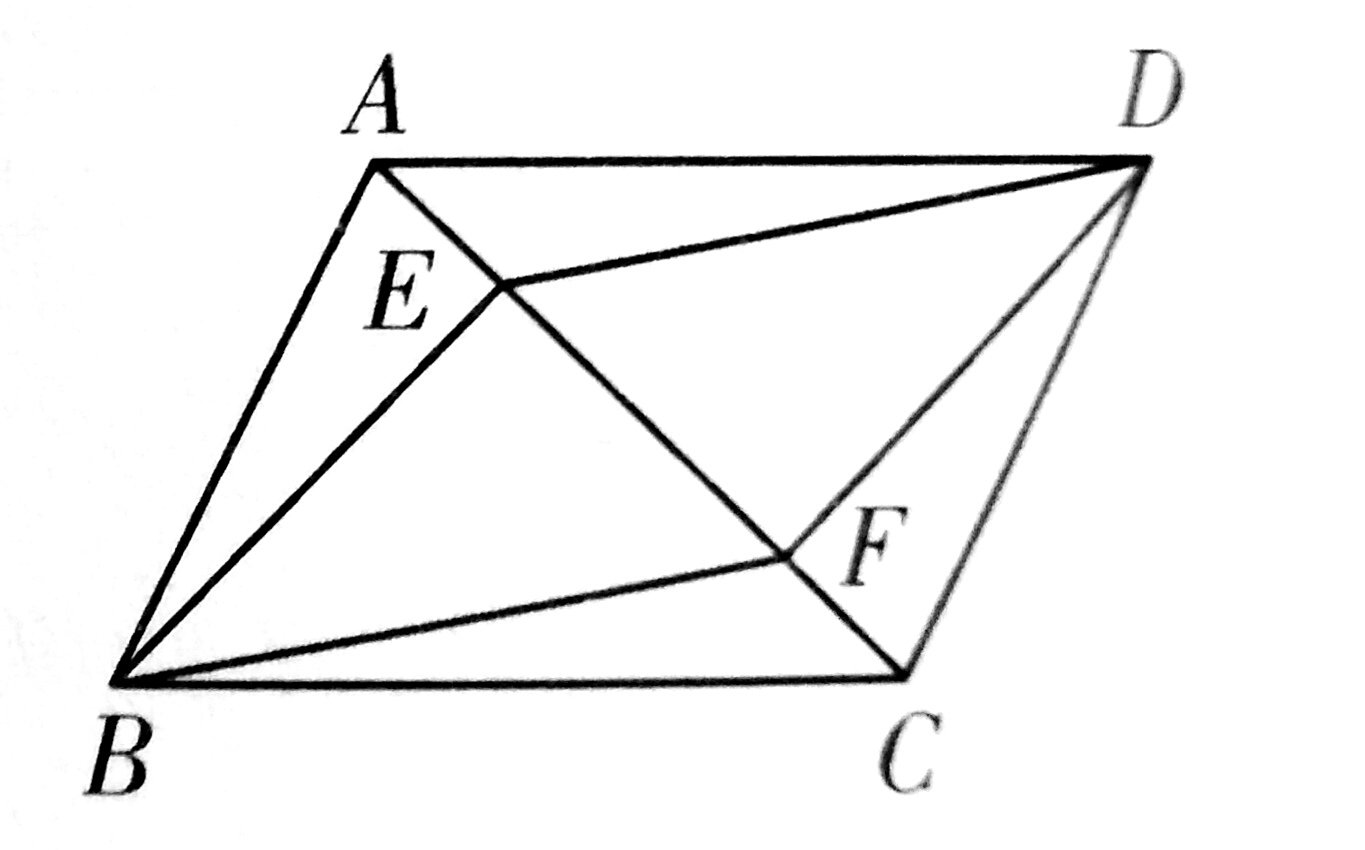
2、如图，E、F是平行四边形ABCD的对角线AC上的两点，且BE⊥AC，DF⊥AC，连接BE，ED，DF，FB。
(1)求证：四边形BEDF为平行四边形
(2)若BE=4，EF=2，求BD的长。
                                                                                                                 
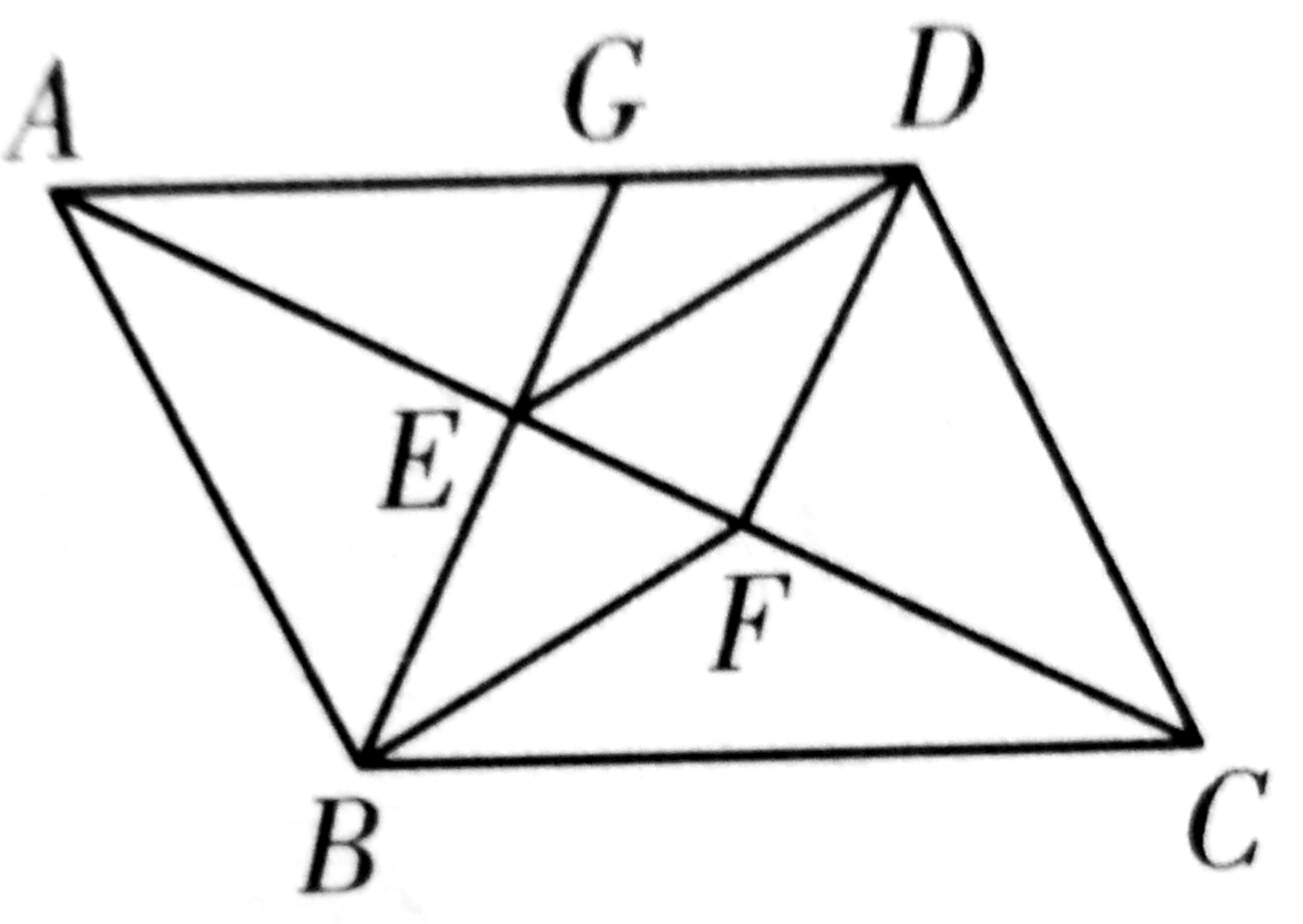
3、如图，四边形ABCD中，BE⊥AC交AD于点G，DF⊥AC，垂足为点F，已知AF=CE，AB=CD。
(1)求证：四边形ABCD是平行四边形
(2)如果∠GBC=∠BCD，AG=6，GE=2，求AB的长。
                                                                                                                  
参考答案：
1、(1) ∵∠E右=∠C=90°
           ∴DB∥CF
           ∵∠CBF=∠DCB(已知)
           ∴DC∥BF
          ∴DBFC是平行四边形(两组对边平行)
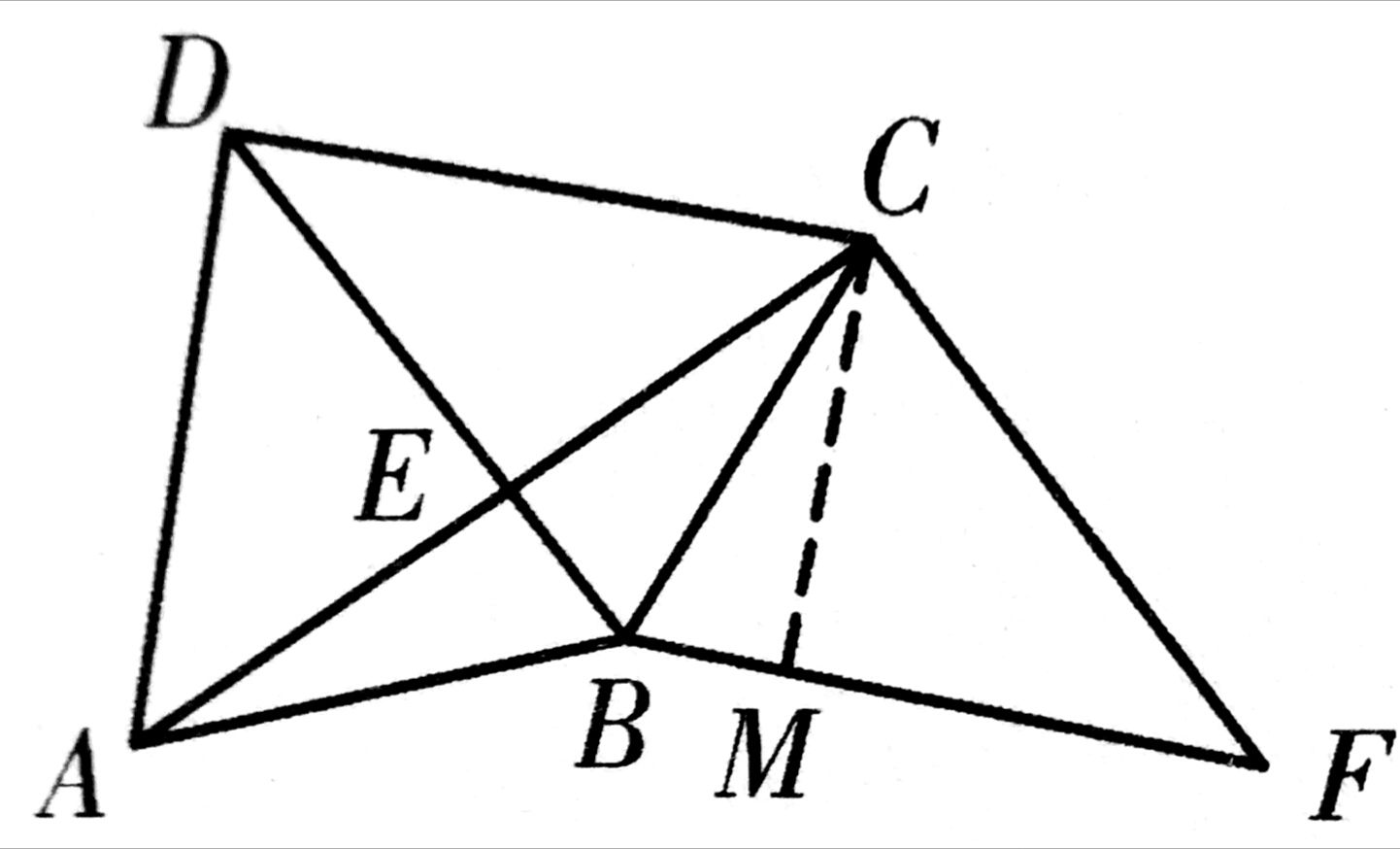
  (2)作CM⊥BF
     ∵CM=CE(角平分线到两端距离相等)
         CM²=CF²—FM²(△MCF中)
         CM=FM(∠F=45°，∠C右=45°)
     ∴2CM²=CF²
       即2CM²=BD²(CF=DB)
           2CM²=2²
               CM=√2
     又∵AE=CE (AB=BC，E垂直)
        ∴AC=√2+√2 (AC=AE+CE，CE=CM)
                 =2√2

2、(1) 连接对角线BD交O
     ∵AB∥DC
    ∴∠BAE=∠DCF(内错角)
    ∵BE⊥AC  DF⊥AC
    ∴∠E左=∠F右 (90°角)
       △ABE和△CDF中
           ∠BAE=∠DCF
            ∠E左=∠F右
                 AB=CD
    ∴△ABE≌△CDF(AAS)
    ∴AE=CF(对应边)
    ∴OE=OF (OA=OC)
  又∵OB=OD(四边形ABCD对角线)
     ∴四边形BEDF为平行四边形

(2) BO²=BE²+EO²(△BEO中)
  即BO²=4²+1²=17
    ∴BO=√17
        BO=DO
    ∴BD=√17+√17=2√17

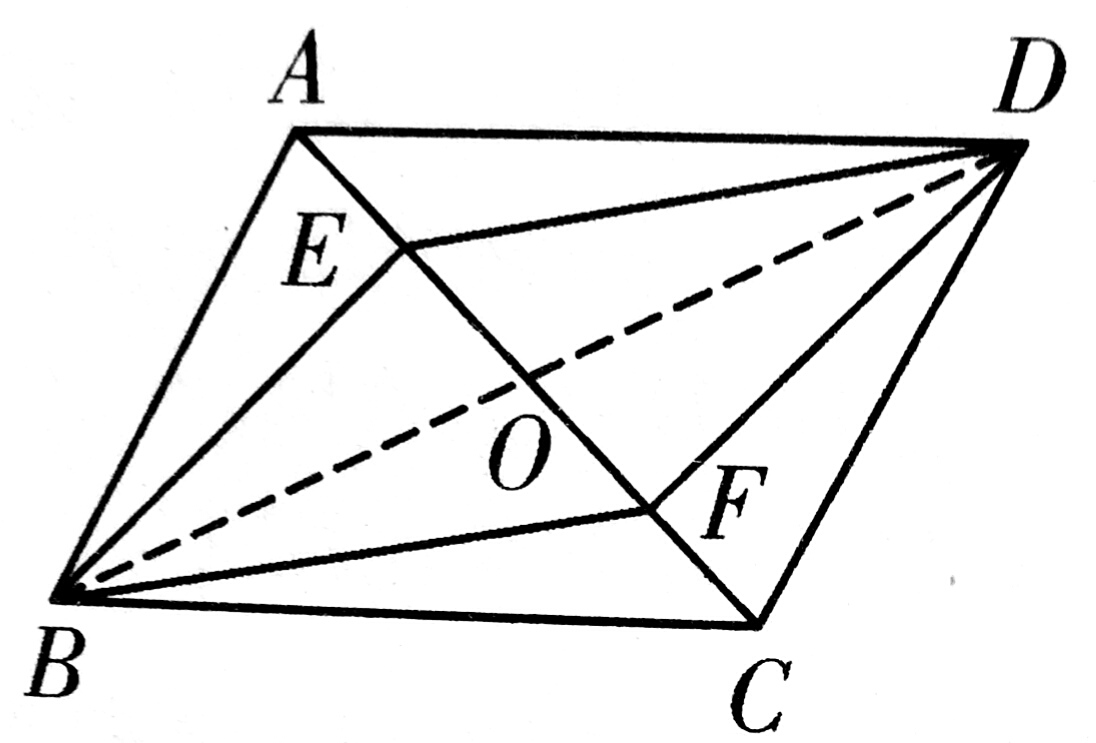
3、(1)∵AF=CE
          ∴AE=CF(同减EF)
       在直角△ABE和直角△CDF中
               AE=CF(已证)
               AB=CD(已知)
     ∴△ABE≌△CDF(HL)
     ∴∠A下=∠C上
     ∴AB∥DC(内错角)
    ∴ABCD是平行四边形(平行且相等)

(2)∵∠GBC=∠BCD
   ∴GDBC是等腰梯形
   ∴GB=DC=AB
     AE=√AG²—GE²=4√2
     BE=GB—GE
 即BE=AB—2 (GB=AB)
   AE²+BE²=AB² (△ABE中)
即(4√2)²+(AB—2)²=AB²
            AB=9

每天学习一小时，快乐工作一辈子。潜龙家教谭老师全程做题并录入，感谢您的光临！