1、如图，AYC 是一条直线，△ABC和△AXY是两个位于AYC两侧的等边三角形，连接BY，XC。
(1)求证：△ABY≌△ACX
(2)证明：△CXY的周长等于AC+BY。
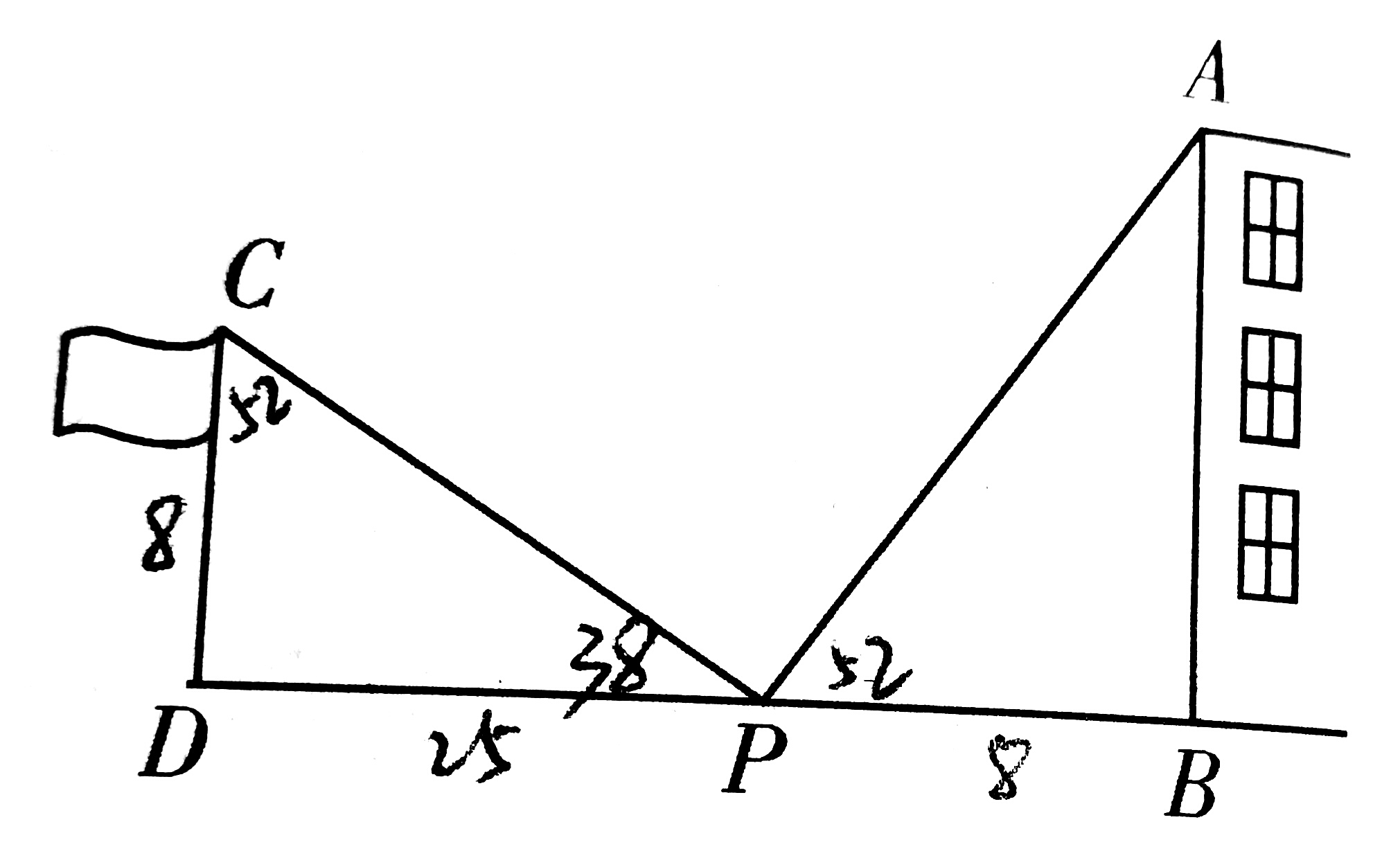
2、为了测量一幢高楼的高AB，在旗杆CD与楼之间选定一点P，测得旗杆顶C的视线PC与地面夹角∠DPC=38°，测得楼顶A的视线PA与地面夹角∠APB=52°，量得P到楼底距离PB与旗杆高度相等，为8m。量得旗杆与楼之间距离为DB=33 m，请计算楼高AB。
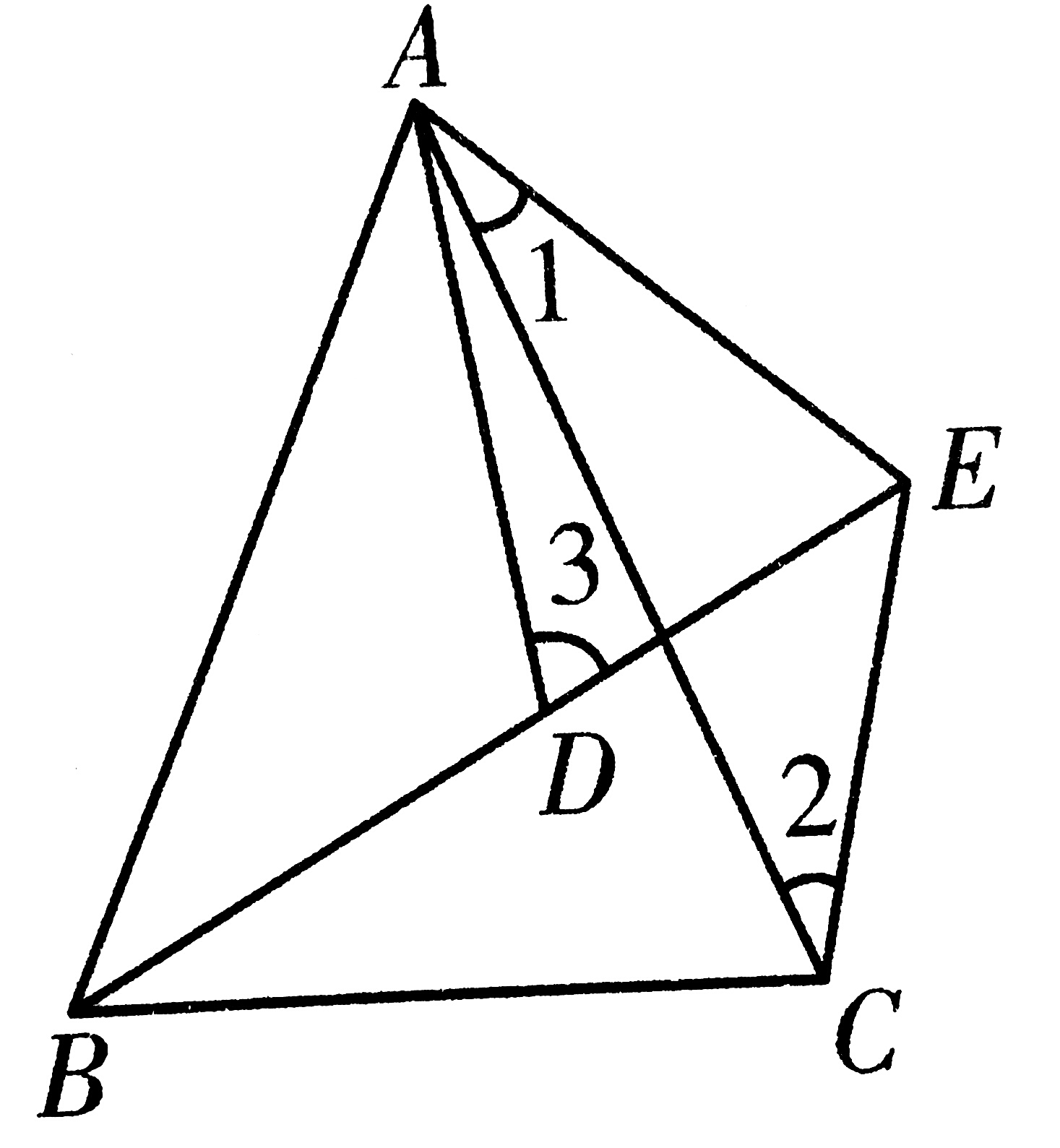
3、广西北流市试题。如图，已知AB=AC，AD=АЕ，BD=CE,，且B，D，E三点共线，求证：∠3=∠1+∠2。
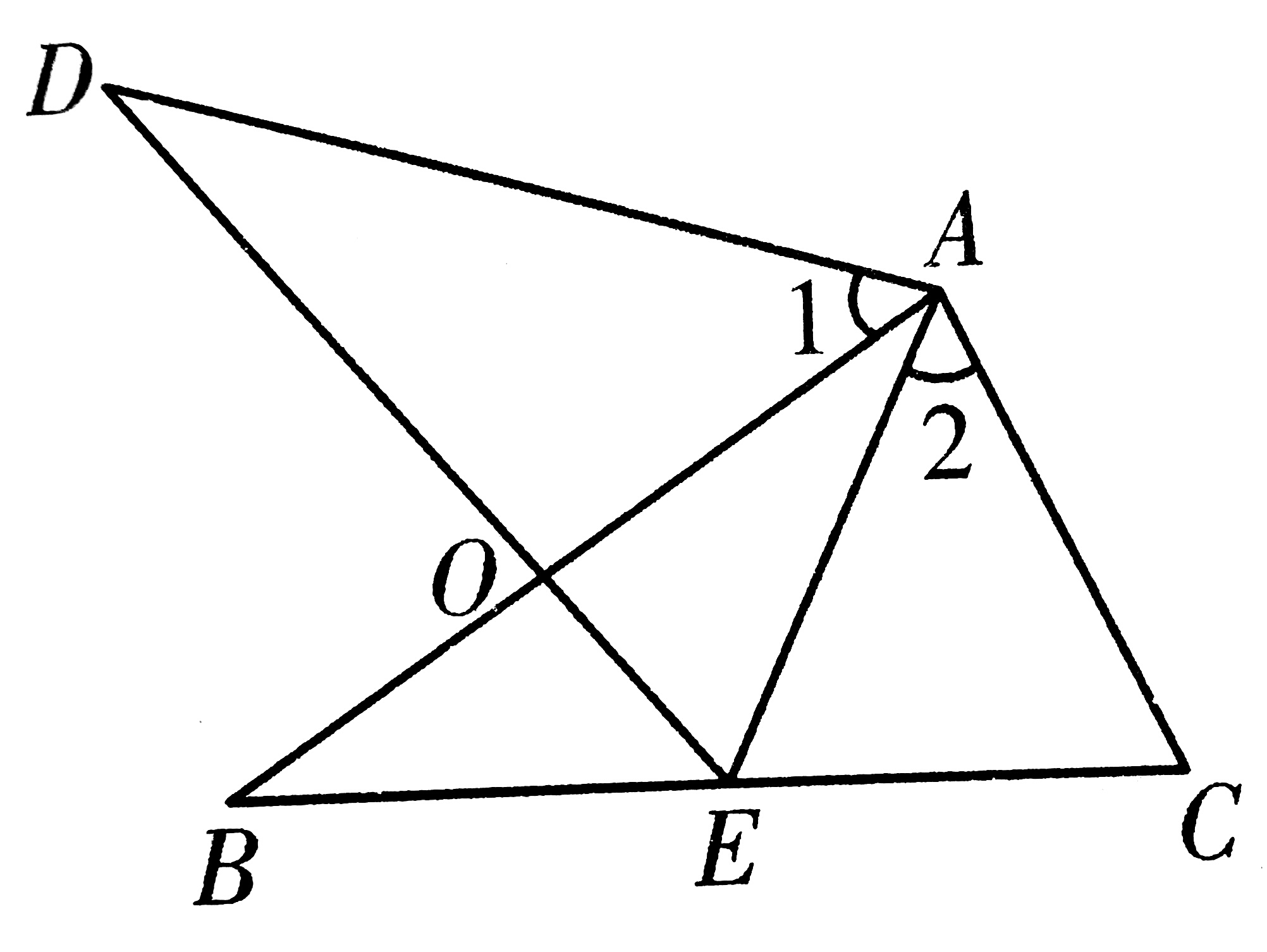
4、如图所示，∠1=∠2，AB=AD，点E在边BC上，∠C=∠AED，AB与DE相交于点O。
(1)求证：△АВС≌△ADE
(2)∠1=40°时，求∠BED的度数。

                   
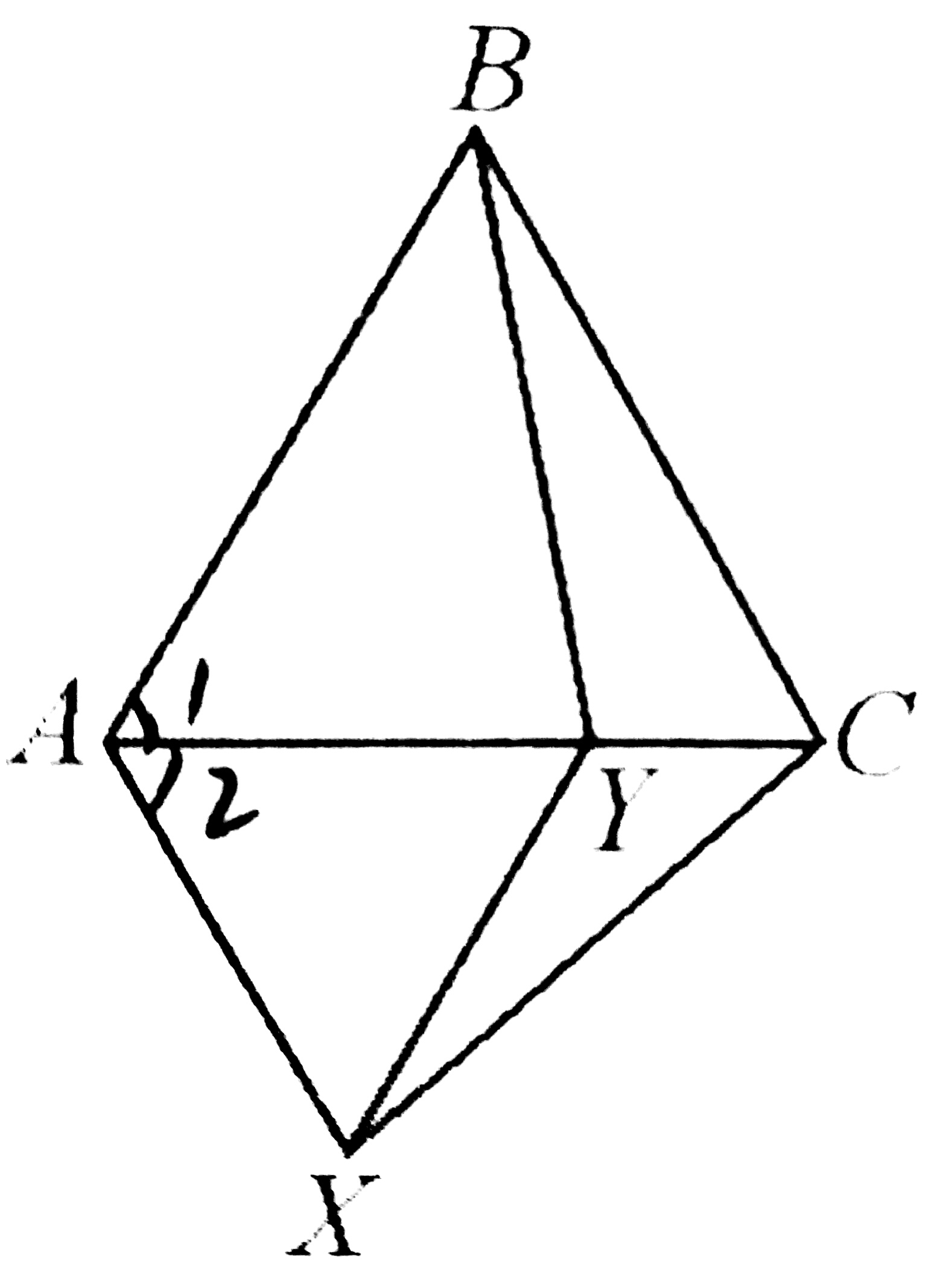
参考答案：
1、(1)∵△ABC和△AXY是等边三角形
          ∴AB=AC
             ∠1=∠2
              AY=AX
          ∴△ABY≌△AXC(SAS)
      (2)△CXY周长=XY+YC+XC
           ∵XY=AY(等边三角形)
              XC=BY(全等三角形)
            ∴△CXY周长=AY+YC+BY
               而AY+YC=AC
             ∴△CXY周长=AC+BY
2、∵∠P左=38°，∠D=90°
     ∴∠C=52°
     在△CDP和△APB中
      ∵∠C=∠P右(已证)
           CD=PB(已知)
          ∠D=∠B(已知)
       ∴△CDP≌△APB(ASA)
      ∴DP=AB
          DP=DB—PB
      即DP=33-8=25
       ∴AB=25
3、△ABD和△ACE中
  ∵AB=AC AD=AE BD=CE
   ∴△ABD≌△ACE(SSS)
    ∴∠ADB=∠AEC
  又∵∠ADB+∠3=180°(邻补角)
         ∠AEC+∠1+∠2=180°(△AEC中)
        ∴∠3=∠1+∠2
4、(1)∵∠E=∠C(已知)
            ∠DAE=∠BAC(由∠1=∠2加公共角得出)
             AB=AD(已知)
         ∴△ABC≌△ADE(AAS)
    (2)在△DAO和△OBE中
         ∵∠D=∠B(已证)
              ∠O处是一对对顶角
         ∴∠BED=∠1=40°

潜龙家教谭老师全程解题并录入，时间精力所限，错误之处请您指正，感谢！