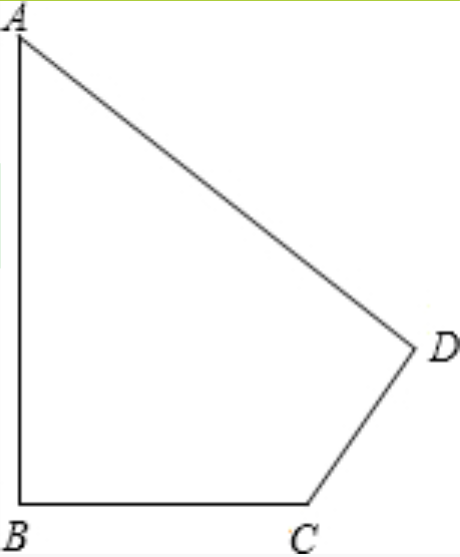
1、如图，已知一块四边形的草地ABCD，其中∠B=90°，AB=20 m，BC=15 m，CD=7m，DA=24m，求这块草地的面积。

2、如图，有一个水池，水面是一个边长为10分米的正方形，在水池正中间有一根芦苇，它高出水面1分米，如果把这根芦苇拉向水池边缘，它的顶端恰好到达池边的水面。请问水的深度与这根芦苇的长度分别是多少？

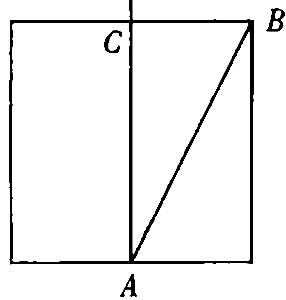
3、如图，有一个圆柱，它的高为13 cm，底面周长为10cm，在圆柱的下底面A点处有一只蚂蚁，想吃到对面距离上底面1cm处B点的食物，那么蚂蚁需要爬行的最短路程是多少厘米？
                                             
【参考答案】：
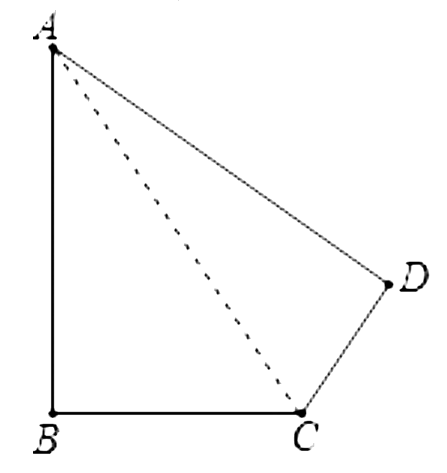
1、连接AC
   ①直角△ABC中
    AC²=AB²+BC²
    ⇨AC=20²+15²
        AC=25
    ②△ACD中
       ∵25²=24²+7²
       ∴△ACD是Rt△。
    ③S△ABC=底×高×1/2=15×20×1/2=150
        S△ACD=底×高×1/2=7×24×1/2=84
             150+84=234m²
2、如图，正中间的芦苇拉向边缘，刚好构成一个直角三角形：Rt△ABC。
   AC=水深   AB=芦苇长度   CB=中间到边缘距离
              AC²+CB²=AB²
        AC²+(10÷2)²=(AC+1)²
                        AC=12
                   AB=12+1=13
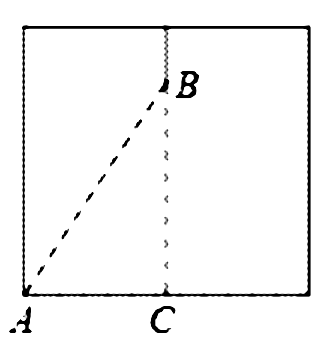
3、将圆柱体展开，得到右下角图形，最短路径是AB。
      AC=半圆周长   即=10÷2=5
      BC=圆柱高—低于1厘米处=13—1=12
       AB²=AC²+BC²
       AB²=5²+12²
        AB=13
                                                                   
潜龙家教谭老师全程解题并录入，时间仓促、精力有限，错漏之处请您指正，感谢！