1、“同位角相等，两直线平行”是_____。
A.公理                  B.定理                 C.定义                 D.待证的命题
2、四边形 ABCD 中，若∠B+∠C=180°，则AB与CD的关系是_____。
A.相交                  B.平行                 C.垂直                  D.重合
3、下列命题中，是假命题的是_____。
A.平面内,若a//b，a⊥c,则b⊥c
B.两直线平行，同位角相等
C.负数的平方根是负数
D.若³√a=³√b，则a=b
4、下列命题是假命题的是_____。
A.49的平方根是±7
B.点M(1,a)和点N(3,b)是一次函数y=—2x+1图像上的两点，则a>b
C.无限小数都是无理数
D.点(—2,3)到y轴的距离是2
5、在△ABC中，若∠A-∠C=∠B，则△ABC是_____。
A.等边三角形      B.锐角三角形     C.钝角三角形        D.直角三角形
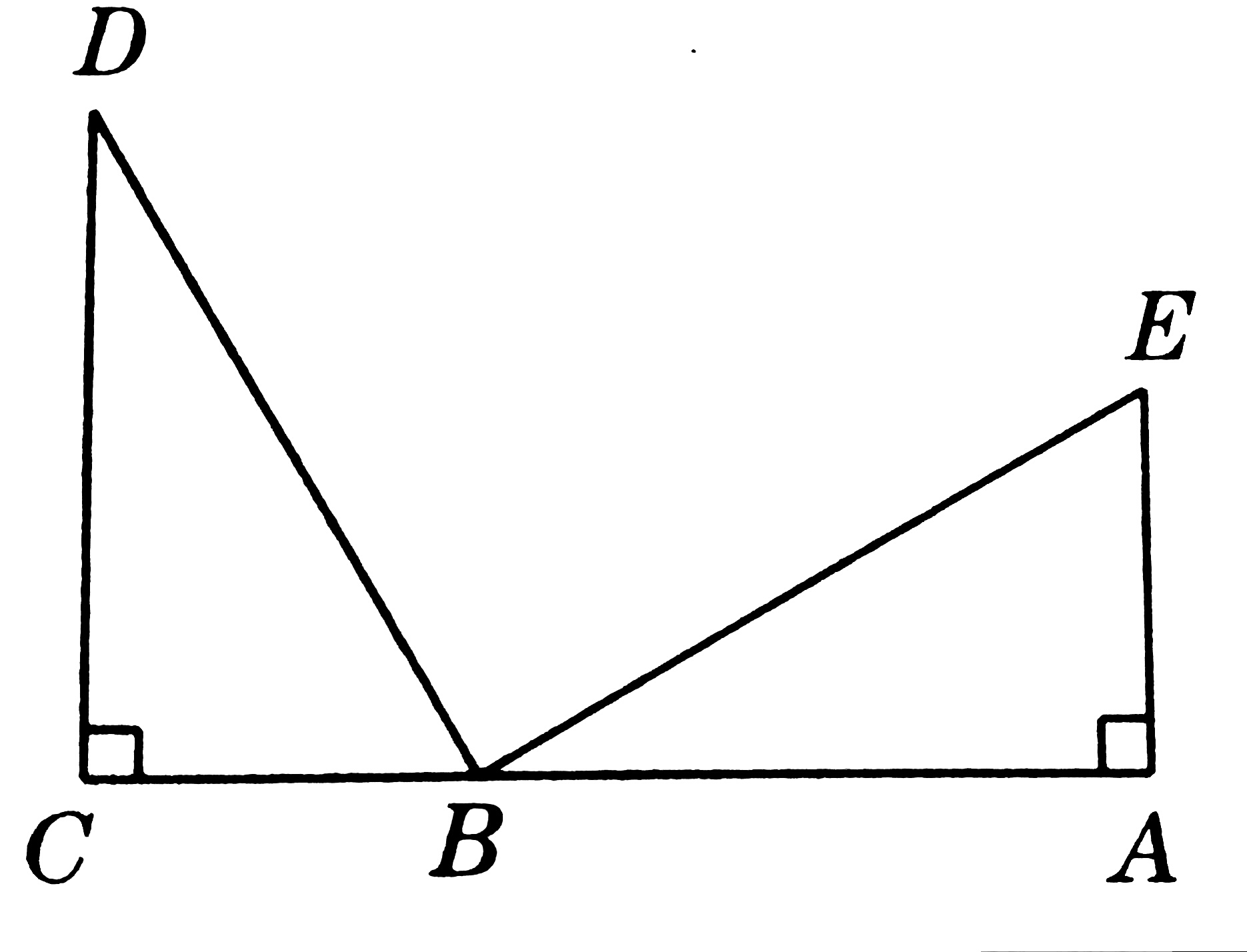
6、如图，DC⊥CA，EA⊥CA，DB⊥ЕB，DB=BE。求证：
(1)△BCD≌△ABE    (2)AC=CD+AE
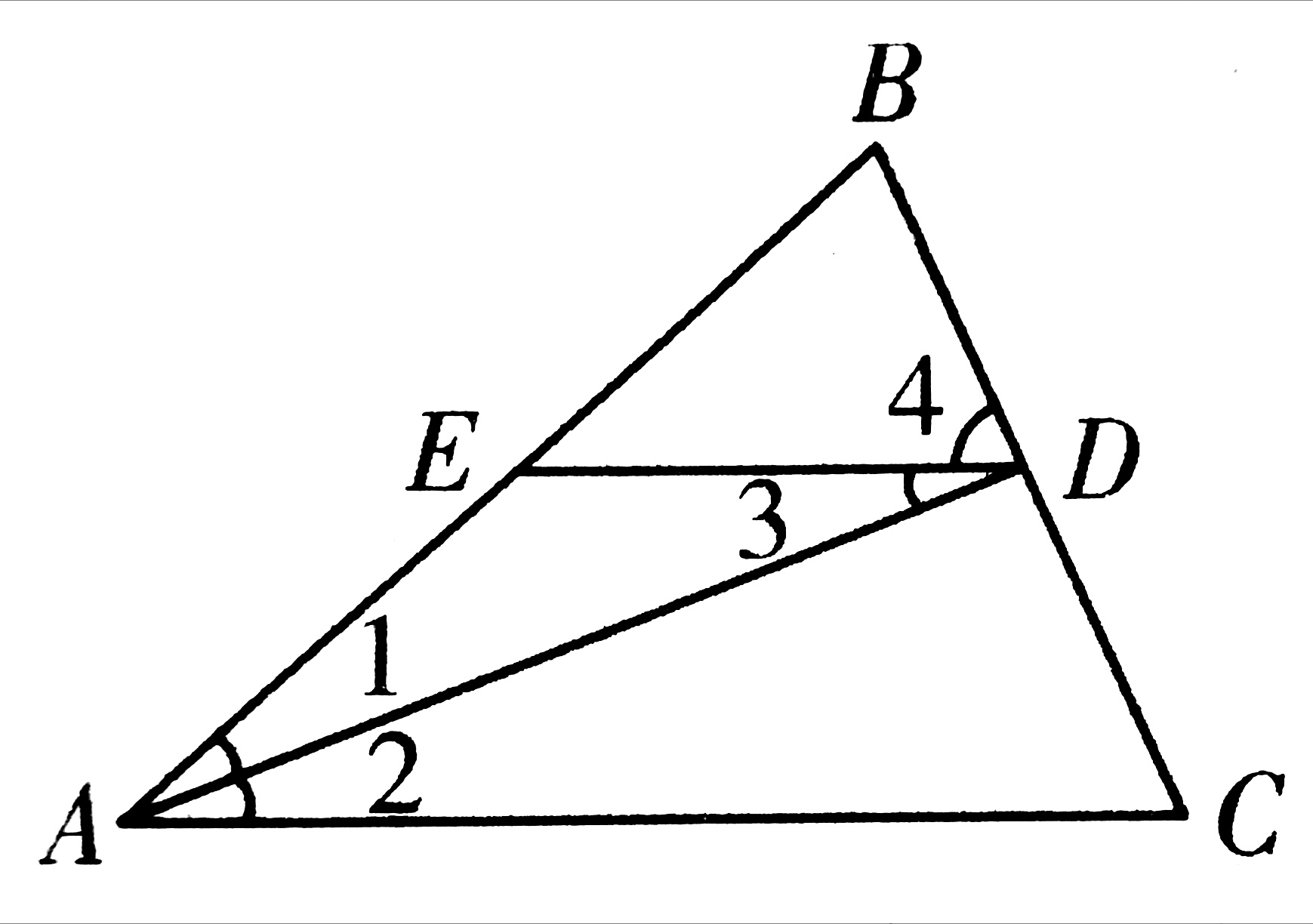
7、在△АВC中，AD平分∠BAC交BC于点D，在AВ上取一点E，使EA=ED。
(1)求证：DE // АC。
(2)若ED=EB，BD=2，EA=3，求AD的长。
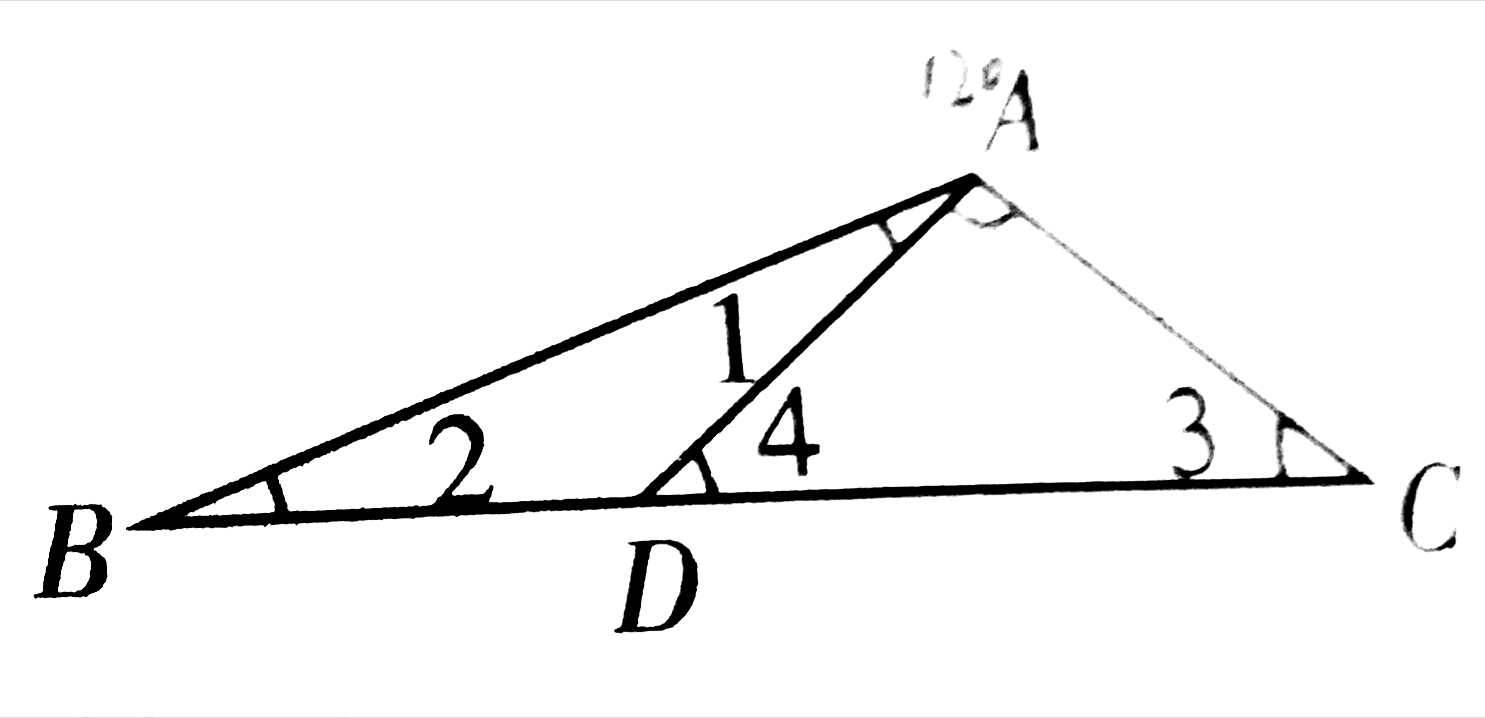
8、已知：如图，在△ABC中，D为BC上一点，∠1=∠2，∠3=∠4，∠BAC=120°，求∠DAC的度数。
                                
            第6题图                                          第7题图                                 第8题图

参考答案：1-5 ABCCD
6、(1)∵∠B左=∠B右=90°(DB⊥EB,平角)
         ∴∠B左+∠D=90°(△BCD内角和)
         ∴∠B右=∠D(等量代换)
             △BCD和△ABE中
             ∠D=∠B右(已证)
             ∠C=∠A    (已知)
              DB=BE      (已知)
          ∴△BCD≌△ABE(角角边)
 (2)∵CD=AB  AE=BC(对应边相等)
          AC=AB+BC
       ∴AC=CD+AE(等量代换)
7、(1)∵∠1=∠2  EA=ED
          ∴∠1=∠3 (等腰三角形)
          ∴∠2=∠3 (等量代换)
          ∴DE∥AC(内错角相等)
   (2)∵ED=EB   ED=EA
      ∴EB=EA=3
      ∴AB=3+3=6 ∠4=∠B
    又∵∠4=∠C(同位角)
      ∴∠B=∠C
      ∴△ABC是等腰三角形
      又∵AD是角平分线
      ∴AD⊥BC(三线合一)
        直角△ABD中
         AD²+BD²=AB²
        即AD²+2²=6²
                   AD=4√2
8、∵∠4=∠1+∠2(外角)
         ∠4=∠3 (已知)
     ∴∠3=∠1+∠2(等量代换)
   又∵∠1=∠2
     ∴∠3=2∠2(同上)
   又∵∠2+∠3=180°—120°=60°
     ∴∠2+2∠2=60°(等量代换)
     即 3∠2=60° ⇨∠2=20°
     ∴∠DAC=120°—20°=100°

潜龙家教谭老师全程做题并录入，时间精力有限，错漏之处恳请各位不吝指正，谢谢！