1、如图，在钝角△ABC中，已知∠A=135°，AB、AC边的垂直平分线分别交BC于点D,E，交AB,AC 于点F,G。若BD=12，CE=9，求DE的长度。
                                                                                                    
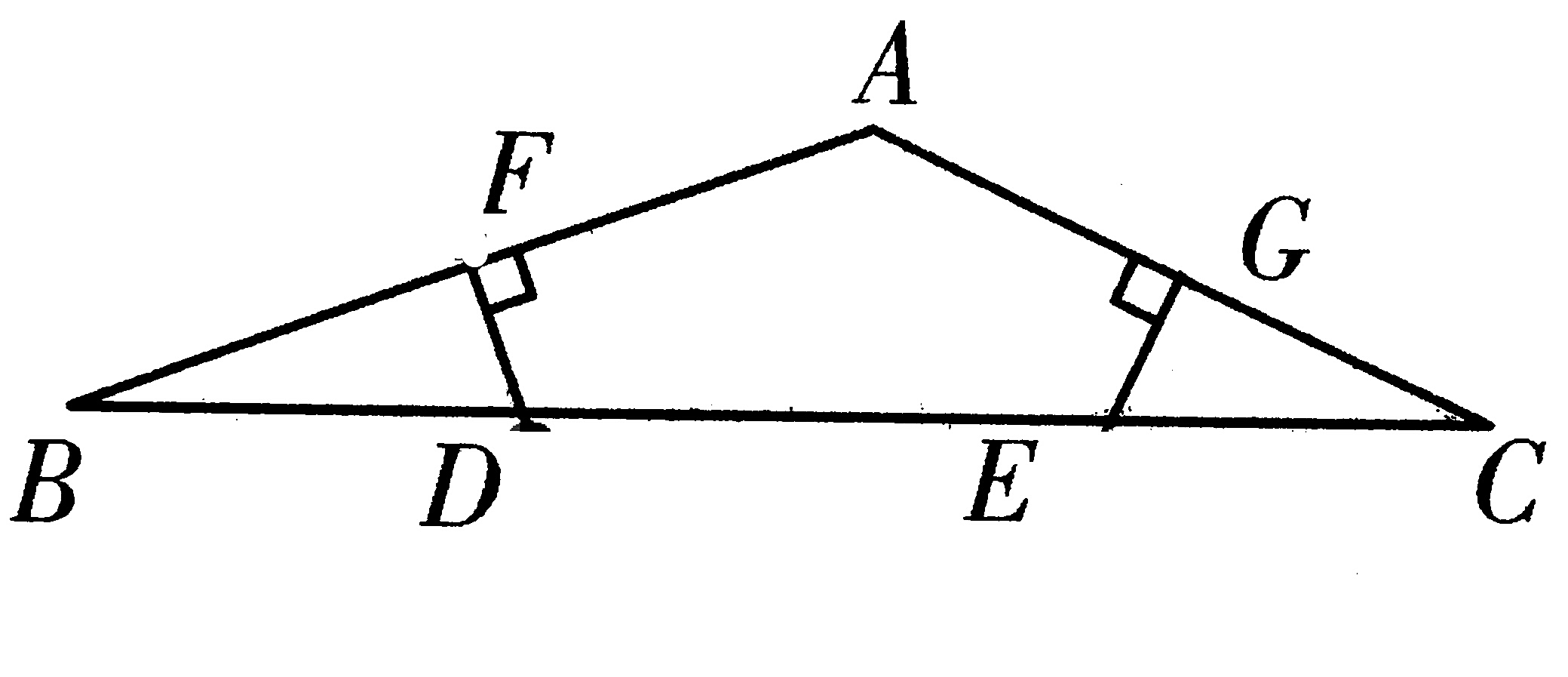
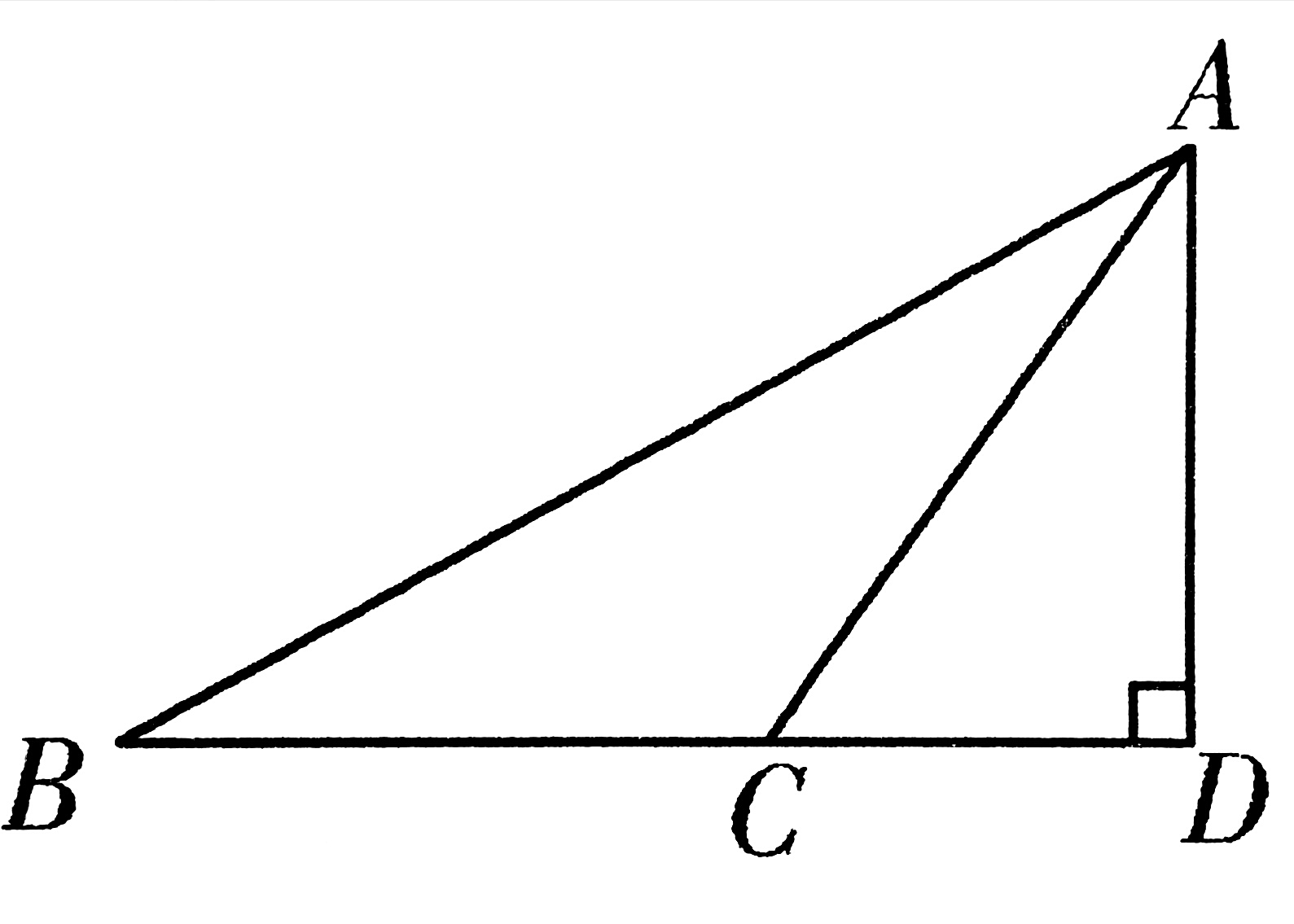
2、如图，在钝角△ABC中，BC=9，AB=17，AC=10，AD⊥BC于D，求AD的长。
                                                                                                  
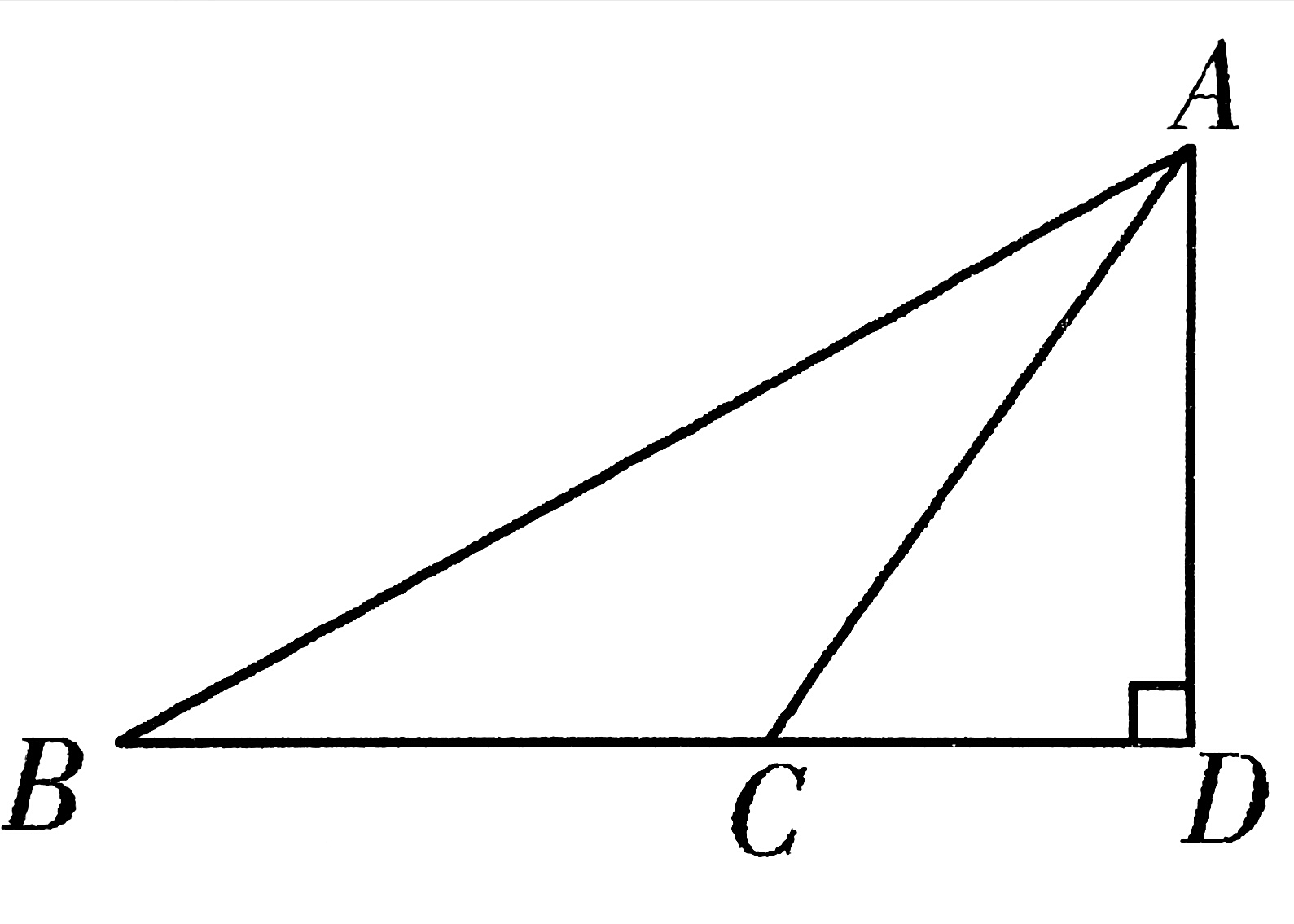
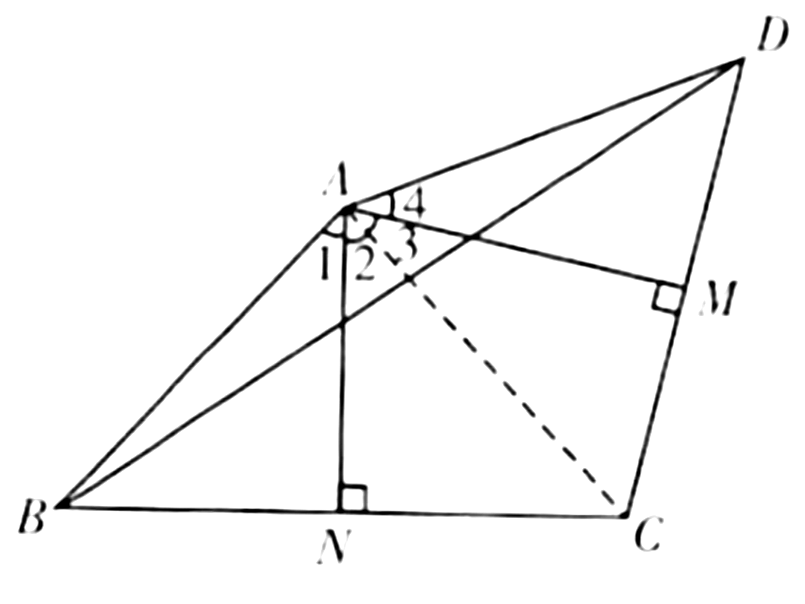
3、如图，在四边形ABCD中，M,N分别是CD,BC的中点，且AM⊥CD，AN⊥BC。
(1)求证：∠BAD=2∠MAN
(2)连接BD，若∠MAN=70°，∠DBC=40°，求∠ADC度数。
                                                                                                  
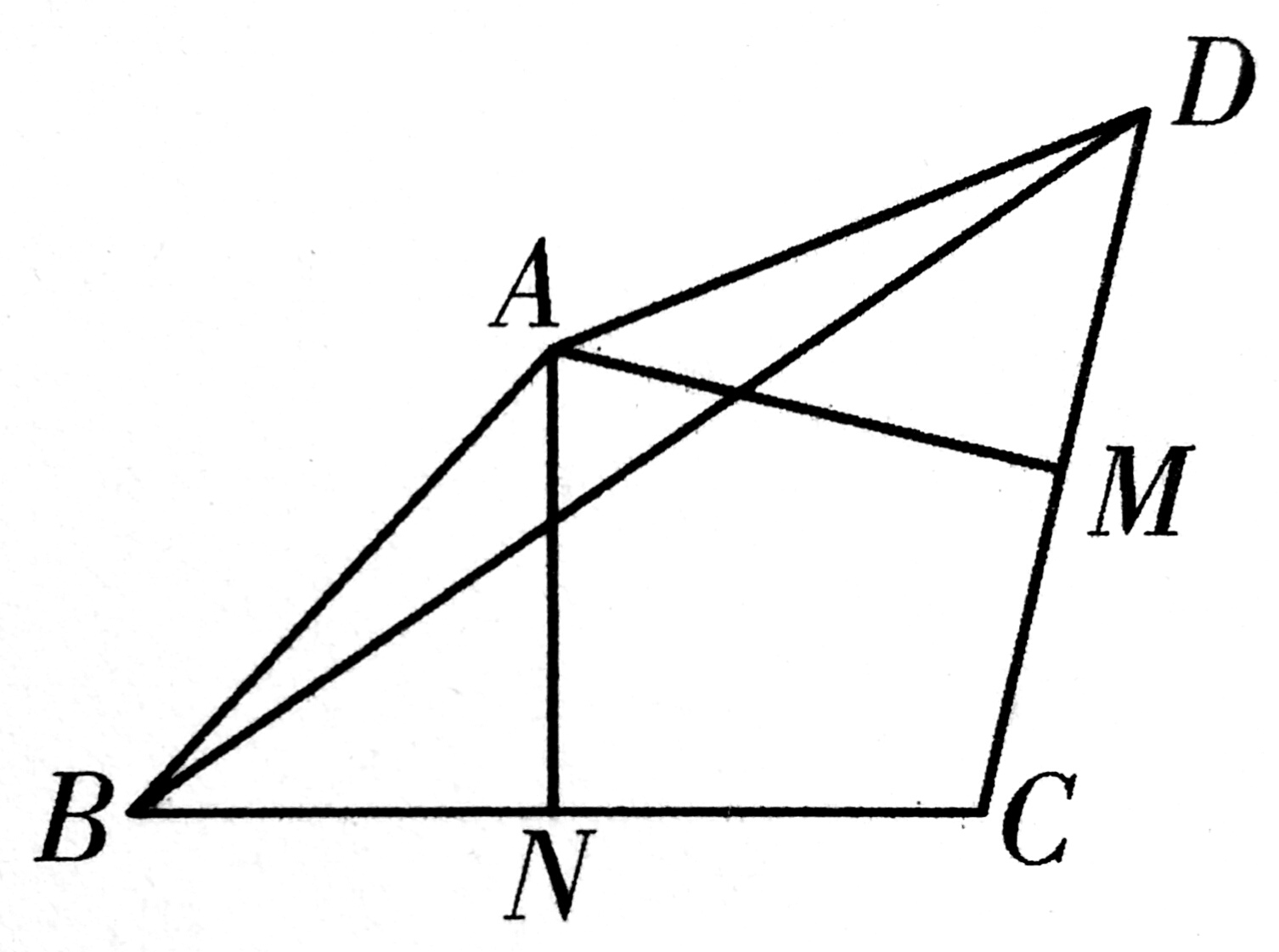
参考答案：
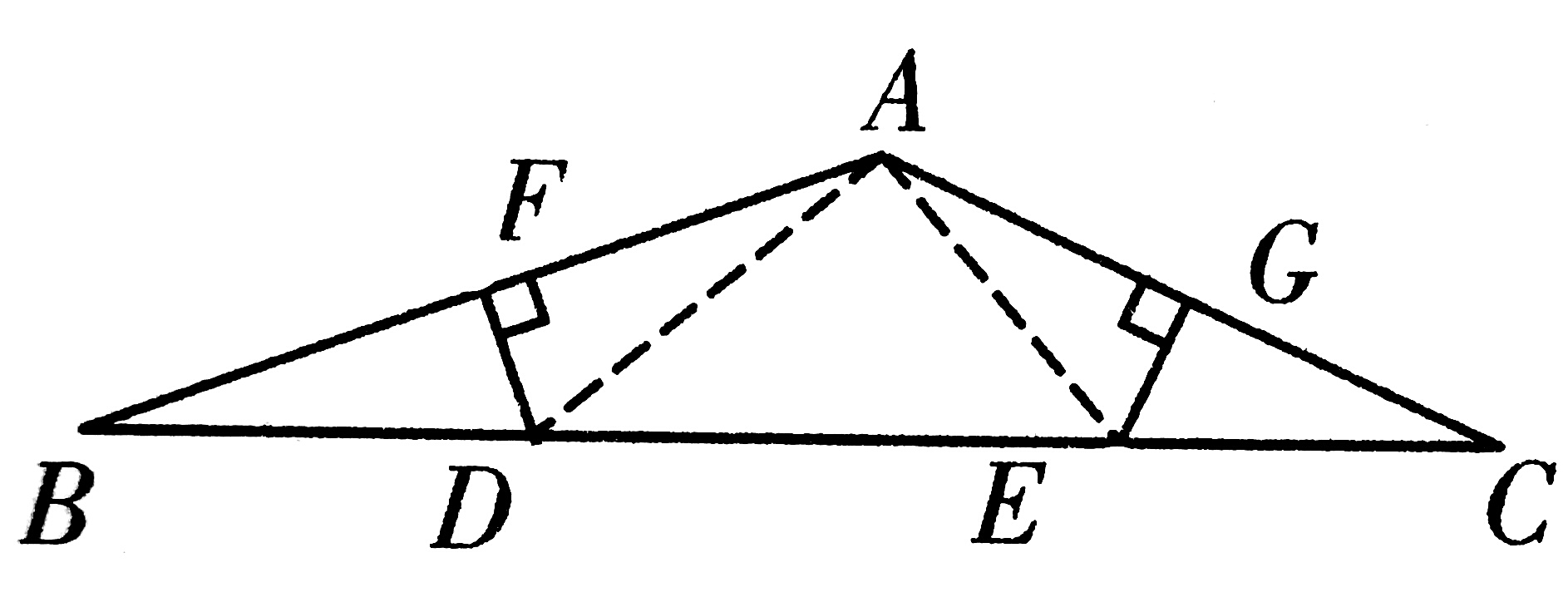
1、连接AD，AE

      ∠B+∠C=180—135=45° (△ABC中)

      ∠B=∠A最左 ∠C=∠A最右  (垂直平分线)    

    ∴∠A最左+∠A最右=45°

    ∴∠DAE=135—45=90° (∠A中)

         DE²=9²+12² (勾股定理，Rt△ADE中)

         DE=15

2、设CD为x，则BD=9+x

     ①BD²+AD²=AB² (△ABD中)

      即(9+x)²+AD²=17²

     ②CD²+AD²=AC² (△ACD中)

       即x²+AD²=10²
     
       以上①—②，得

          18x+81=189

                  x=6

           将x=CD=6代入②

                AD=8

3、连接AC
     (1)∠A₁=∠A₂  ∠A₃=∠A₄

         ∴∠A₂+∠A₃=1/2∠BAD

         ∴∠BDA=2∠MAN

     (2)∠C=360—90—90—70=110°(四边形ANCM中)

   ∴∠D右=180—110—40=30° (△BCD中)

又∵∠BAD=2∠MAN=2·70=140°

       AB=AD  ( AB=AC  AC=AD )

   ∴∠D左=(180—40)÷2=20°

   ∴ ∠ADC=∠D左+∠D右=20+30=50°
                                          
潜龙家教谭老师亲笔解题并录入，时间精力有限，错漏之处恳请批评指正，感谢！