八年级下数学三角形线段垂直平分线习题讲练

【例题讲解】
1、如图，在Rt△ABC中，∠C=90°，∠B=22.5°，AB的垂直平分线交AB于点D，交BC于点E，若CE=3，求BE的长度。
                                                                        
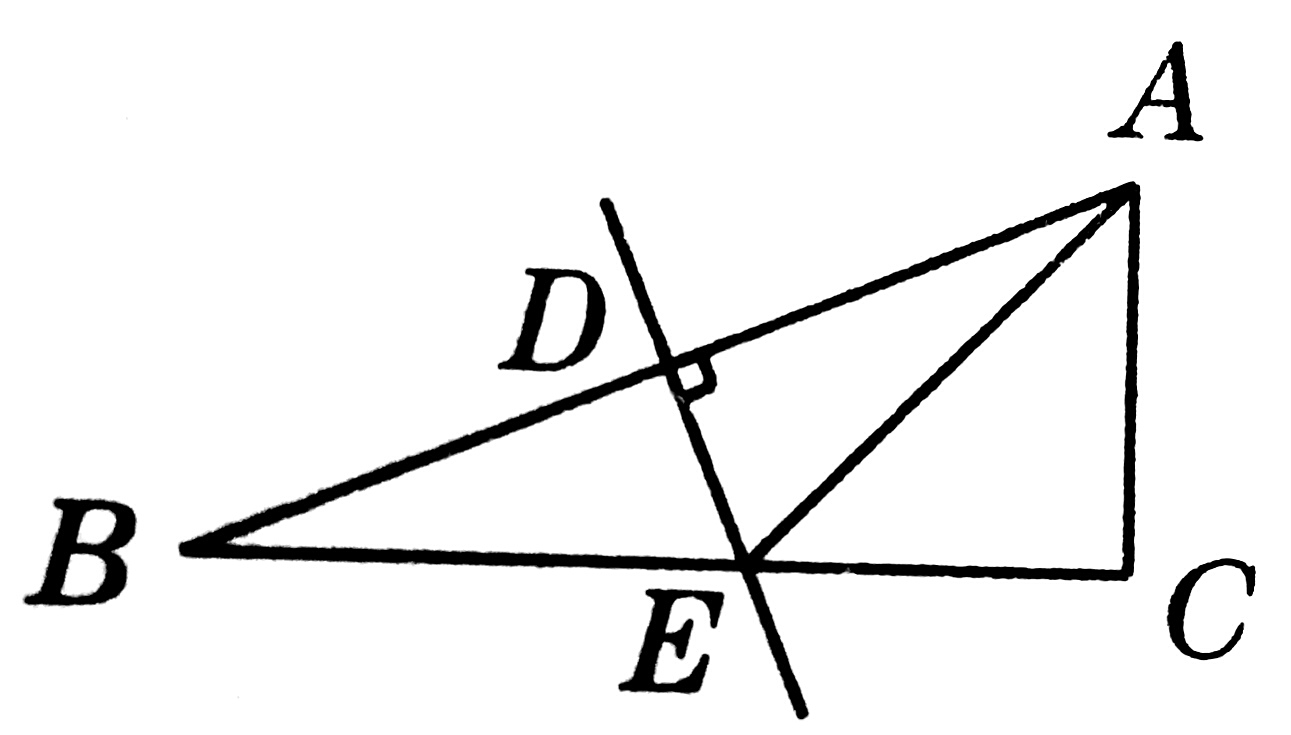
 解：①∵∠A左=∠B=22.5° (垂直平分线)      

                   ∠A=90°—∠B=90—22.5=67.5°
               ∴∠A右=45°
               ∴△ACE是45°的等腰直角三角形
   ②BE=AE (垂直平分线)  
       设AC=CE=x
       x²+x²=AE² (直角△ACE中)
       3²+3²=AE²
             AE=√18
                  =3√2
   答：BE的长度为3√2。

2、如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E。求CE的长度。
                                                                         
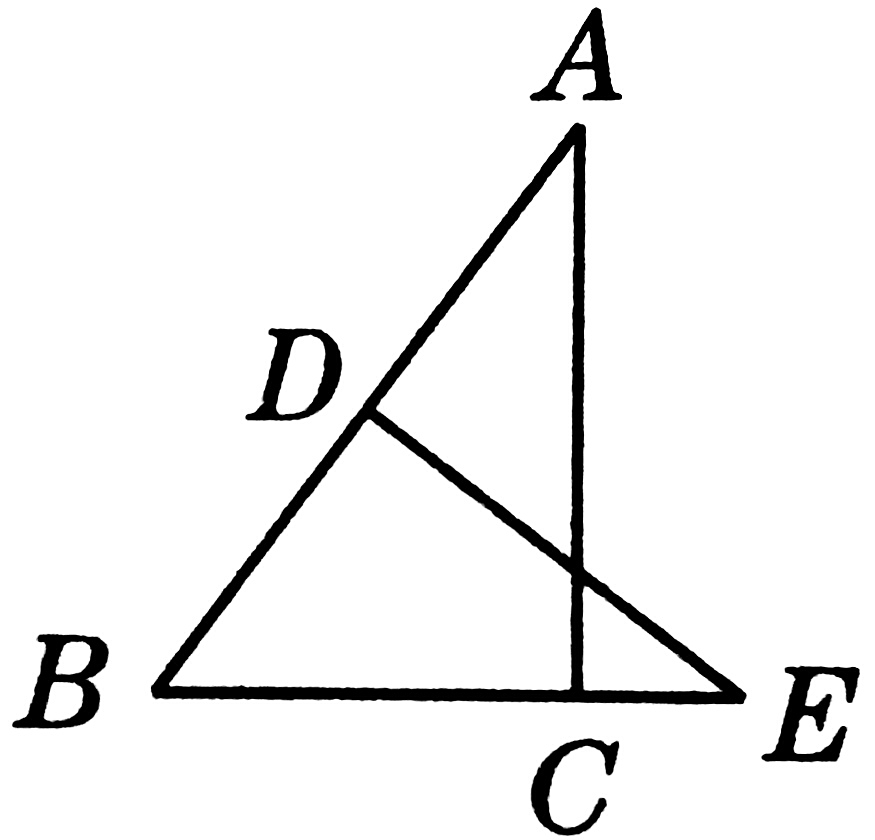
  解：连接AE，设CE=x
        AE=BE=BC+CE=3+x
      AE²=AC²+CE² (△ACE中)
      即(3+x)²=4²+x²
                    x=7/6
  答：CE的长度为7/6。

3、如图，在△ABC中，AB=AC，∠BAC=120°，DE,FG分别是AB,AC的垂直平分线，且BC=12，求EG的长度。
                                                                          
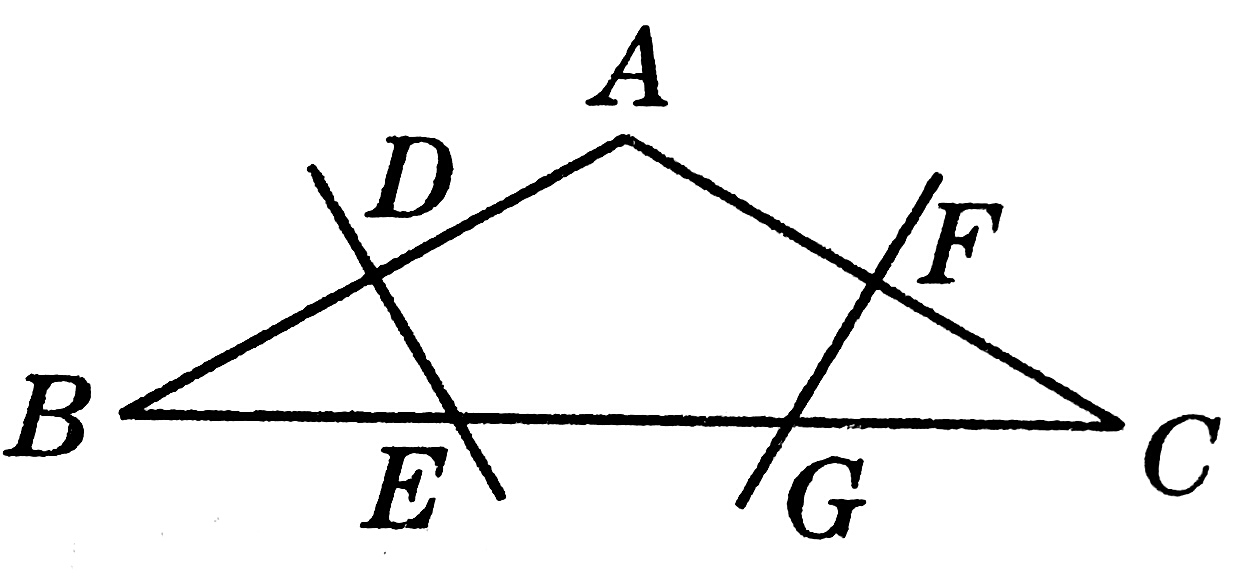
 解：连接AE，AG
①∵∠B=∠C=30° [ 等腰△ABC，(180—120)÷2 ]
 ∠B=∠A左 ∠C=∠A右 (垂直平分线)
∴∠A中=120°—∠A左—∠A右=120—30—30=60°
②∵∠E右=∠B+∠A左=30+30=60° (△ABE外角)
即△AEG中有两个角是60°
∴△AEG是等边三角形
③ BC=△AEG的周长
    EG=BC÷3=12÷3=4
答：EG的长度为4。

【课后练习】
1、如图，在△ABC中，∠C=90°，DE是AB的垂直平分线，AB=2AC，BC=18cm，求BE的长度。
                                                                        
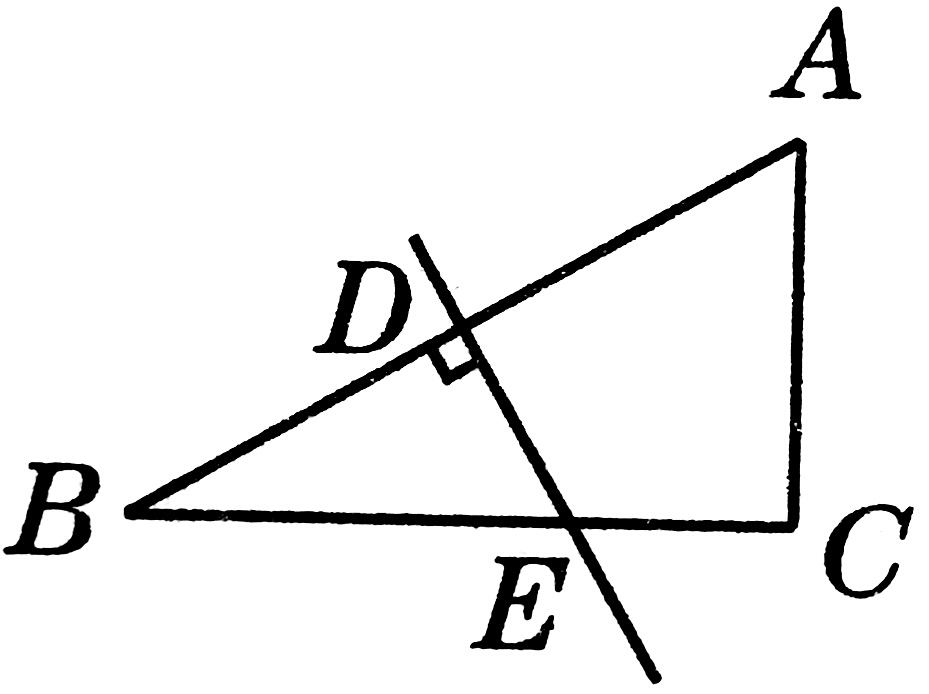
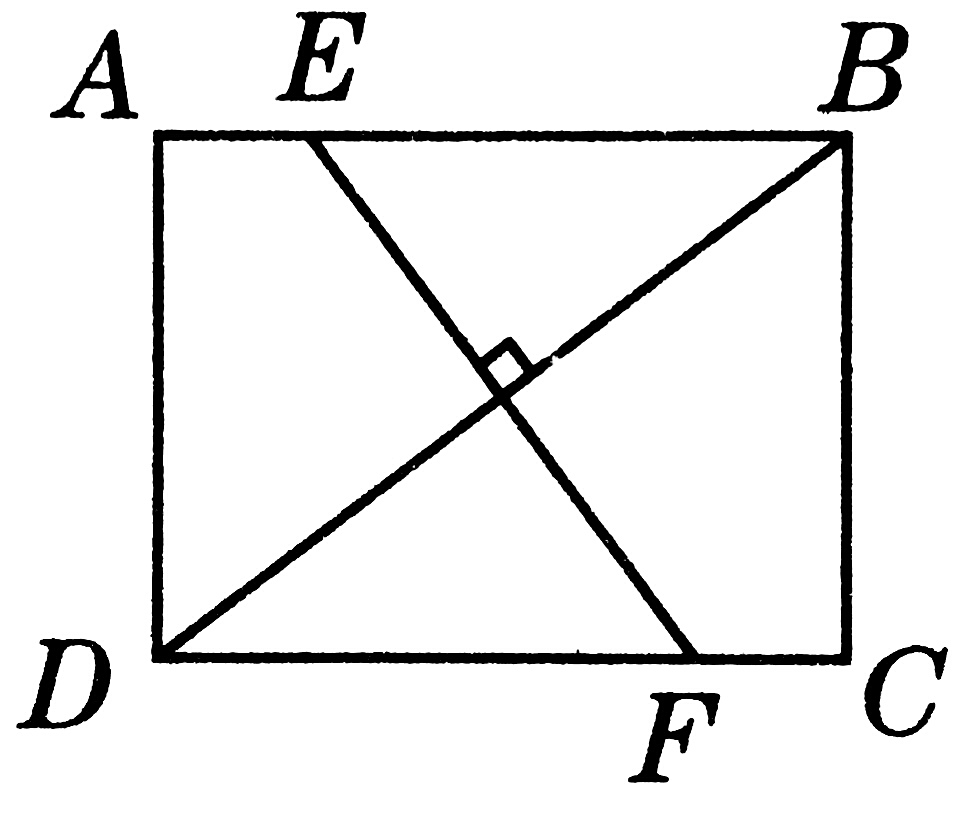
2、如图，在矩形ABCD中，AB=8，AD=6，EF为对角线BD的垂直平分线，求EF的长度。
                                                                       
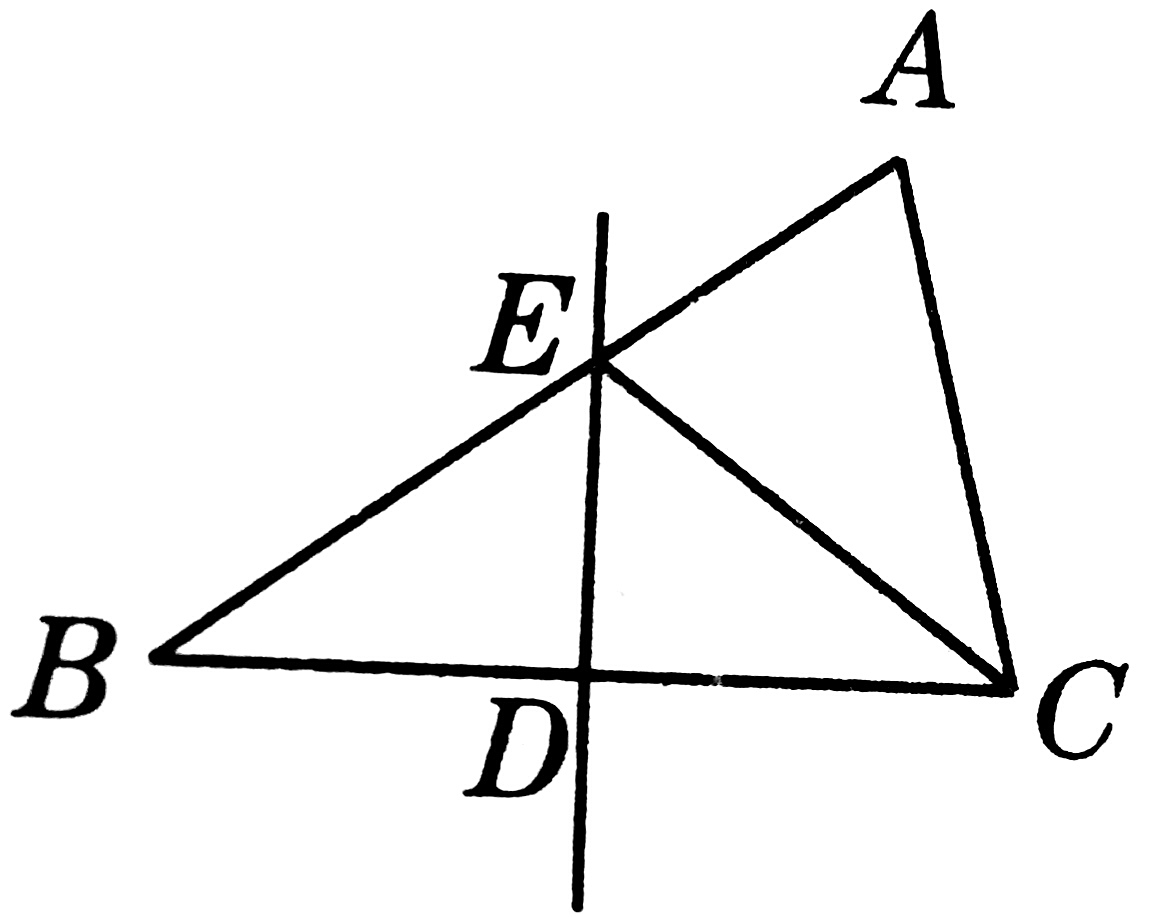
3、如图，在△ABC 中，BC边的垂直平分线DE交BC边于点D，交AB边于点E。若△EDC 的周长为24，△ABC与四边形AEDC的周长之差为12，求线段DE的长度。
                                                                                                          

星光不问赶路人，时光不负追梦人。谭老师解题并录入，课后练习答案:12,7.5,6 感谢！