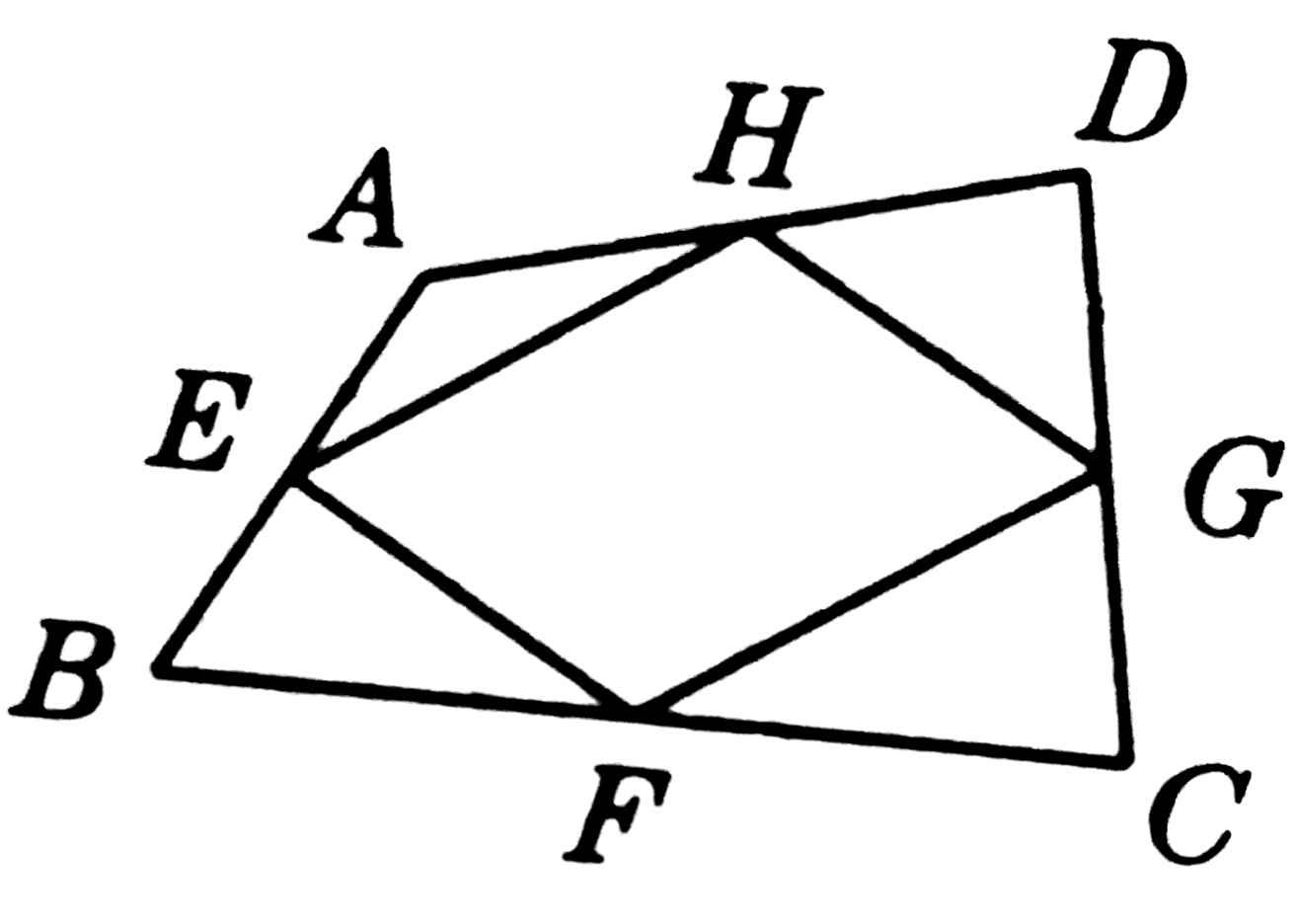
1、如图，在任意四边形ABCD中，E,F,G,H分别是边AB,BC,CD,DA的中点，依次连接各边中点得到四边形EFGH。
(1)这个四边形EFGH的形状是什么？
(2)请证明你以上的结论。
                                                                            
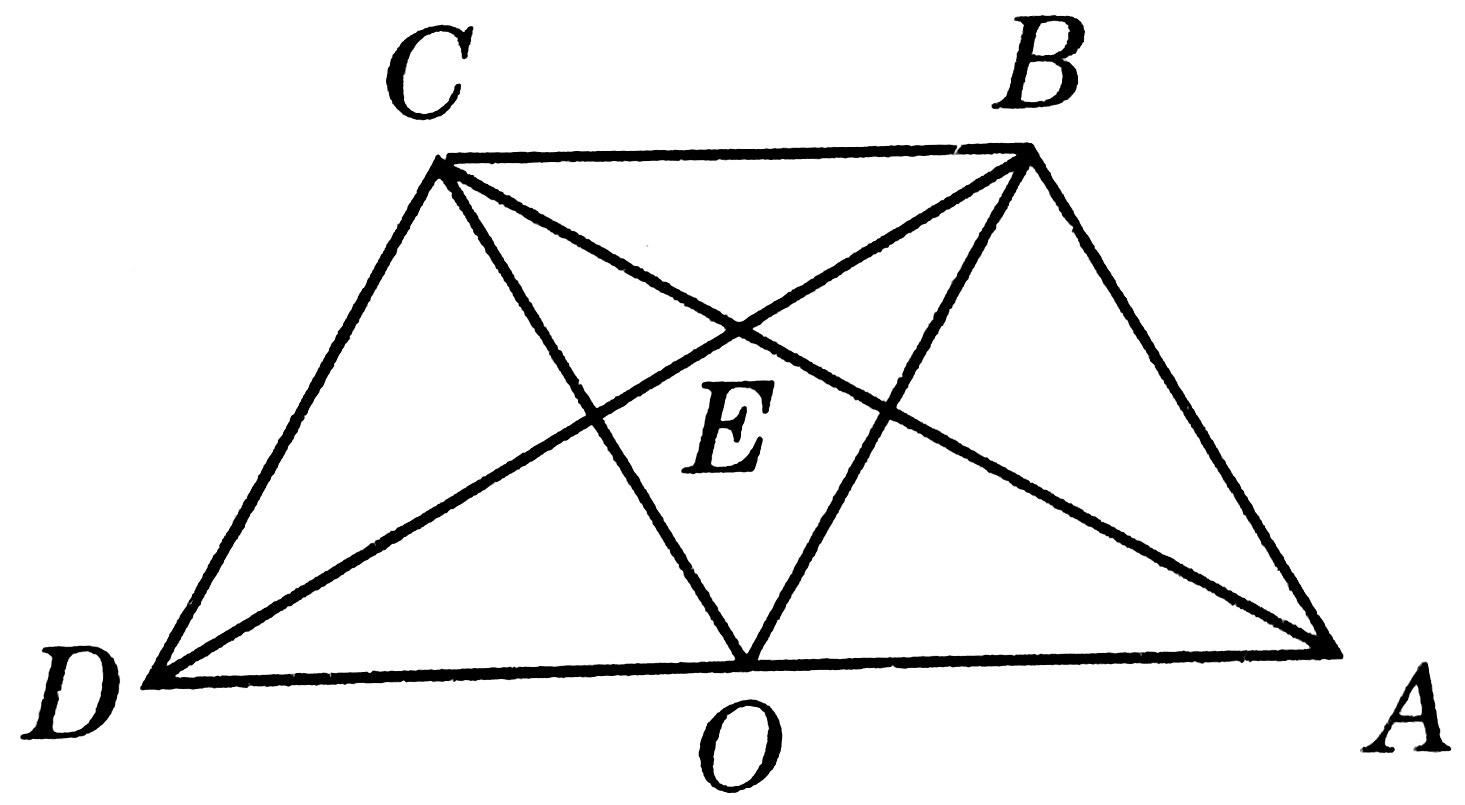
2、如图，O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角形OAB 和等边三角形OCD，连接AC和BD相交于点E，再连接BC。
(1)求∠AEB的大小。
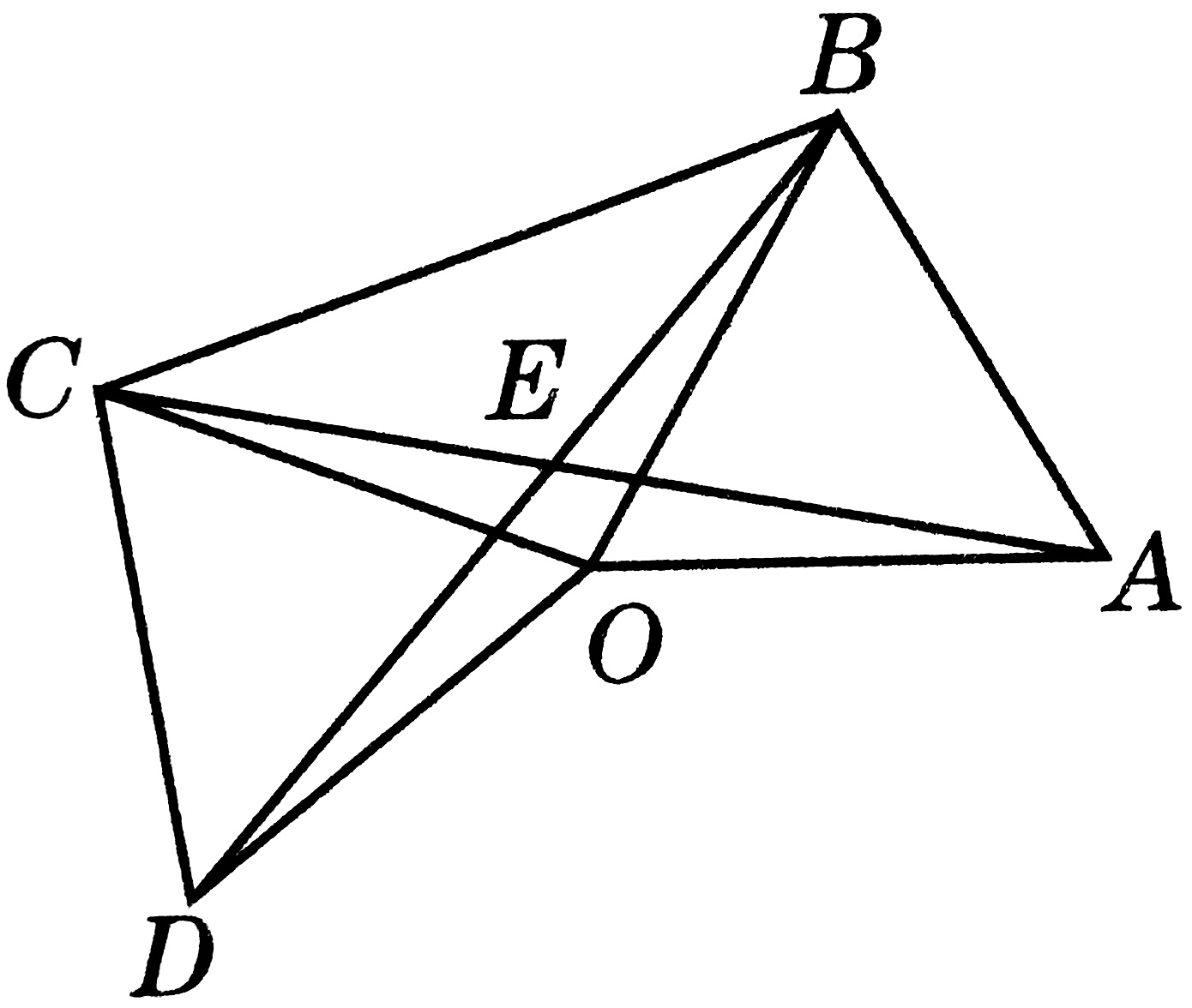
(2)如图，△OAB固定不动，△OCD还是之前的等边三角形，现将△OCD绕点O逆时针旋转一定角度，求此时∠AEB的大小。
                                                                       
【参考答案】
1、(1)这个四边形EFGH的形状是平行四边形。
    (2)证明：连接AC
①∵E、F分别是AB、BC的中点

  ∴EF∥AC   EF=1/2AC (△ABC中)

②又∵H、G分别是AD、DC的中点

   ∴HG∥AC HG=1/2AC (△ACD中)

③综上结果：⇨ EF∥HG EF=HG

  ∴四边形EFGH是平行四边形(一组对边平行且相等)

2、(1)
∵OC=OD
  ∠DOB=∠ COA (60°角+60°公共角)
    OB=OA

∴△DOB≌△COA (SAS)

∴两个三角形的四个锐角都=30°

∴∠AEB=180—90—30=60° (△ABE中，∠ABO=60°)

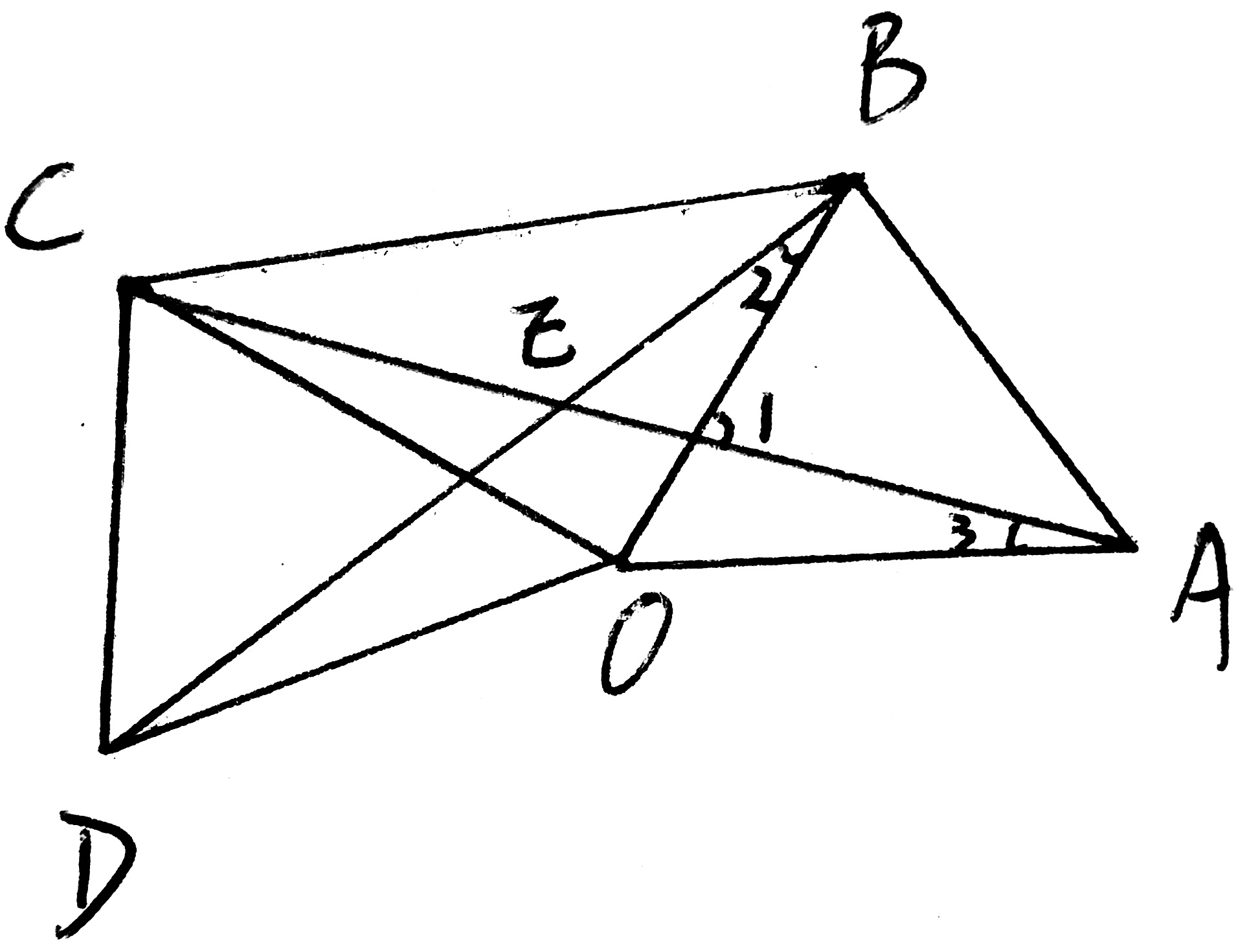
(2)△AOC≌△BOD (方法同上，SAS)

     ∴∠2=∠3

 又∵∠1=∠2+∠AEB (三角形外角)
         ∠1=∠3+∠O右 (三角形外角)

   ∴∠AEB=∠O右=60°
                                                                                               
以上由潜龙家教谭老师全程解题并全程录入，有兴趣的同学请您先自己做做，感谢！