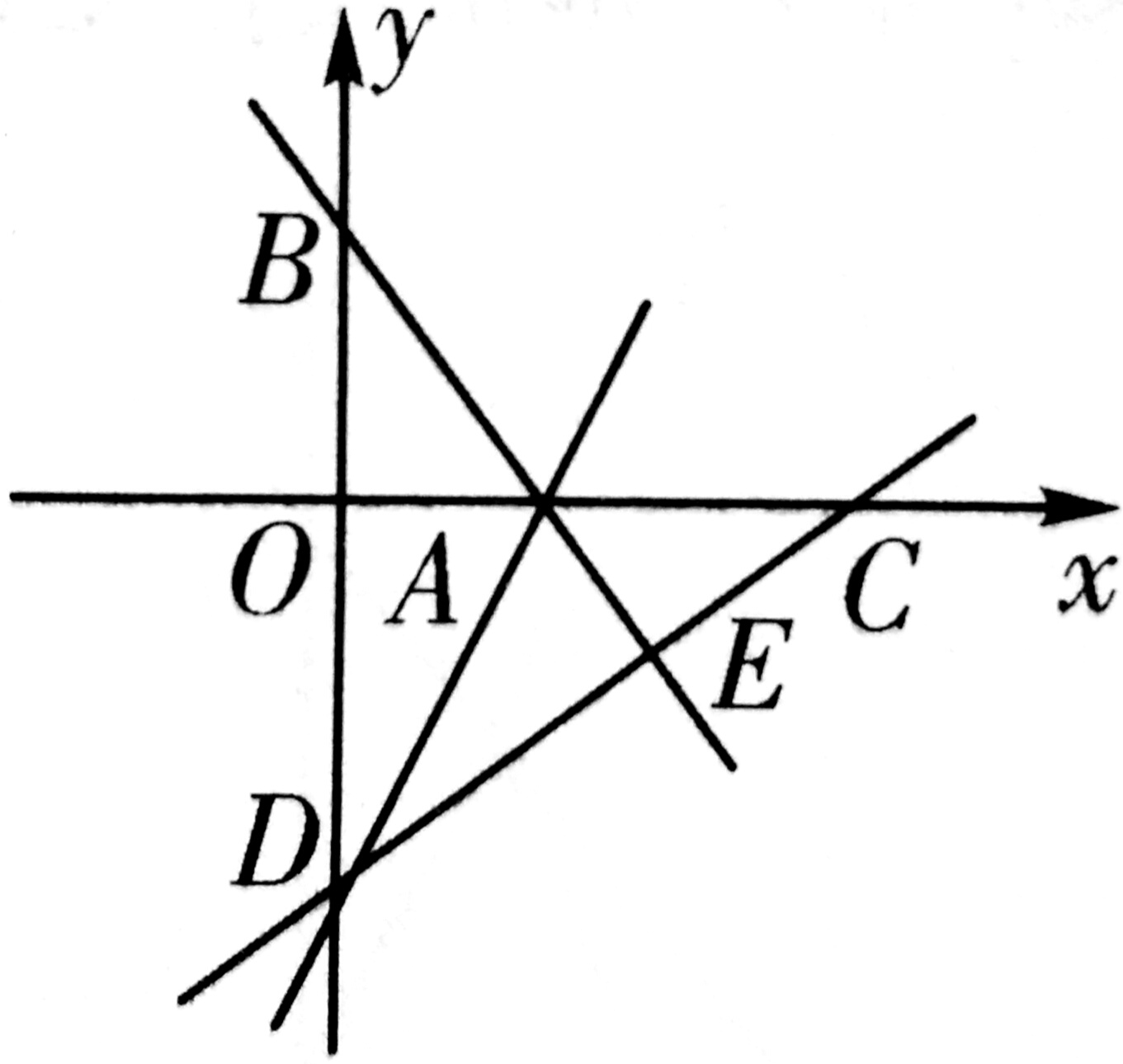
★如图，在平面直角坐标系xOy中，直线y=—4/3x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴的点C处。
(1)①求AB的长 ②点C的坐标
(2)求直线CD的函数表达式
(3)y轴上是否存在一点P，使得S△PAB=1/2S△OCD？若存在，请您求出点P的坐标，若不存在，请说明理由。
                                                     
★讲解：
(1)①由一次函数表达式可知：
        x=0，y=4
        y=0，x=—3
∴B( 0，4)
   A(—3，0)
∴OB=4
   OA=3
∴AB=5

②OA+AC=3+5=8
∴C(8，0)

(2)

  C(8，0)
∴OC=8
     CD=DB
设CD为x，则DC为4+x
△OCD中：x²+8²=(4+x)²
                         x=6
      ∴D(0，—6)
将C(8，0)，D(0，—6)代入y=kx+b，得
            0=8k+b
         —6=0+b
解得  k=3/4
         b=—6
∴y=3/4x—6

(3)谭老师解析：本小题分两种情况：P在y正半轴；P在y负半轴。注意三角形面积公式=底×高÷2，OA始终是△PAB底边PB上的高，且=3。

  S△OCD=6×8÷2=24
∴S△PAB=24÷2=12

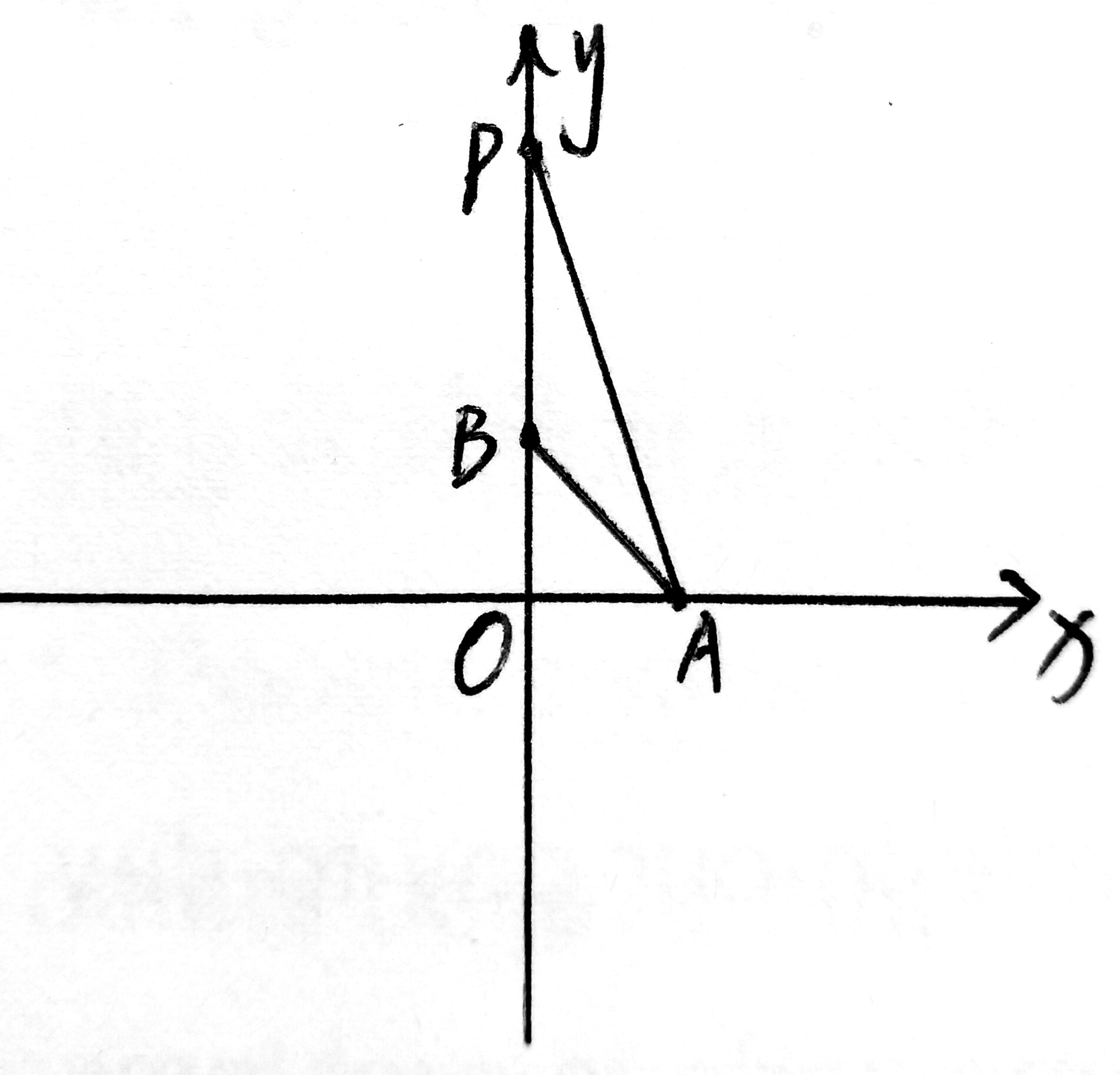
P在y正半轴上：BP×OA÷2=12
                      即 BP×3÷2=12
                                   BP=8
                       OP=4+8=12
                   ∴ P(0，12)
                                                          
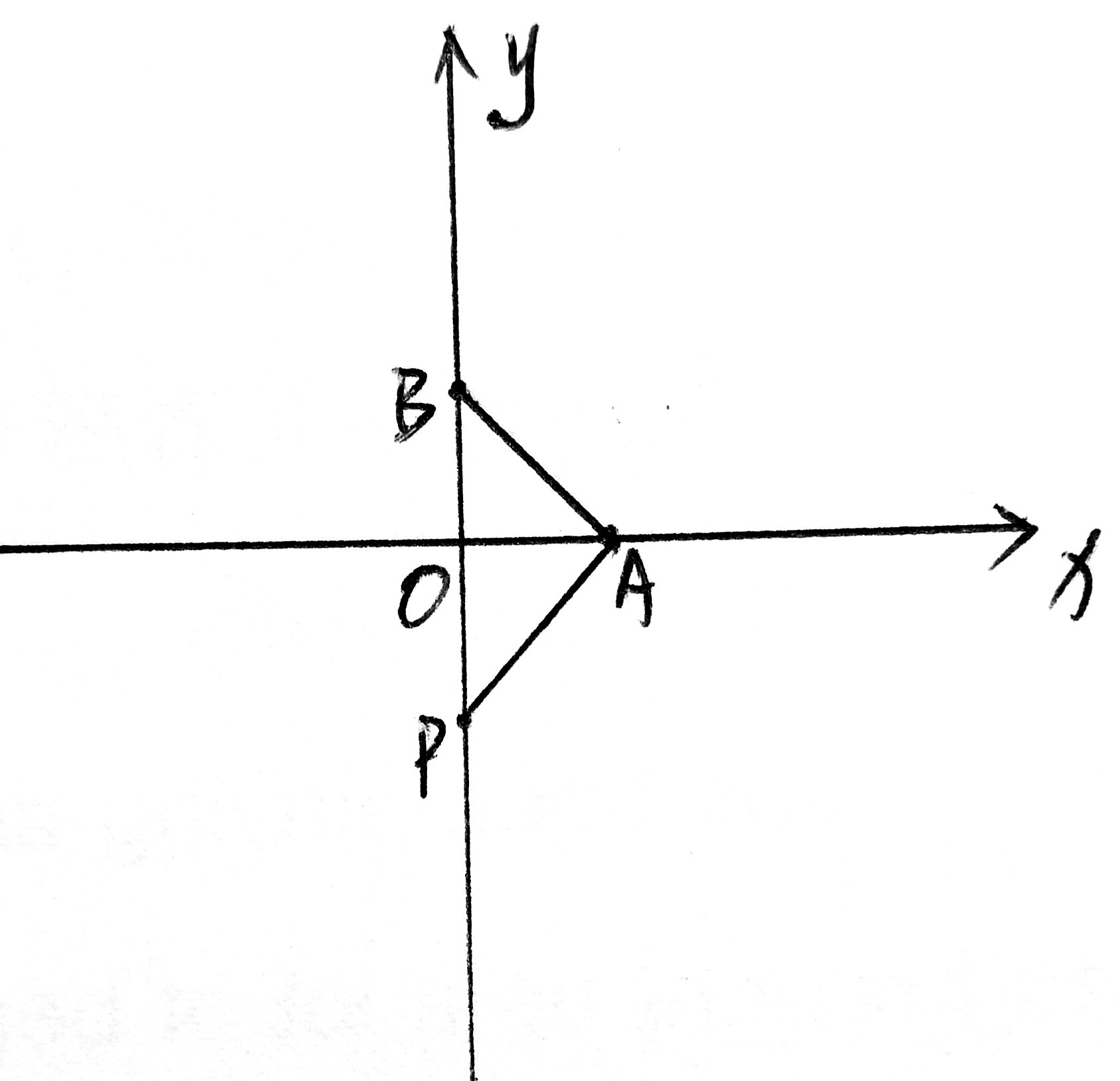
P在y负半轴上：BP×OA÷2=12
                    即 BP×3÷2=12
                         BP=8
           OP=BP—BO=8-4=4
        ∴   P(0，—4)
                                                                                     
★以上全部内容由潜龙家教谭老师全程解题并全程录入，请同学们先自己做一做，谢谢！