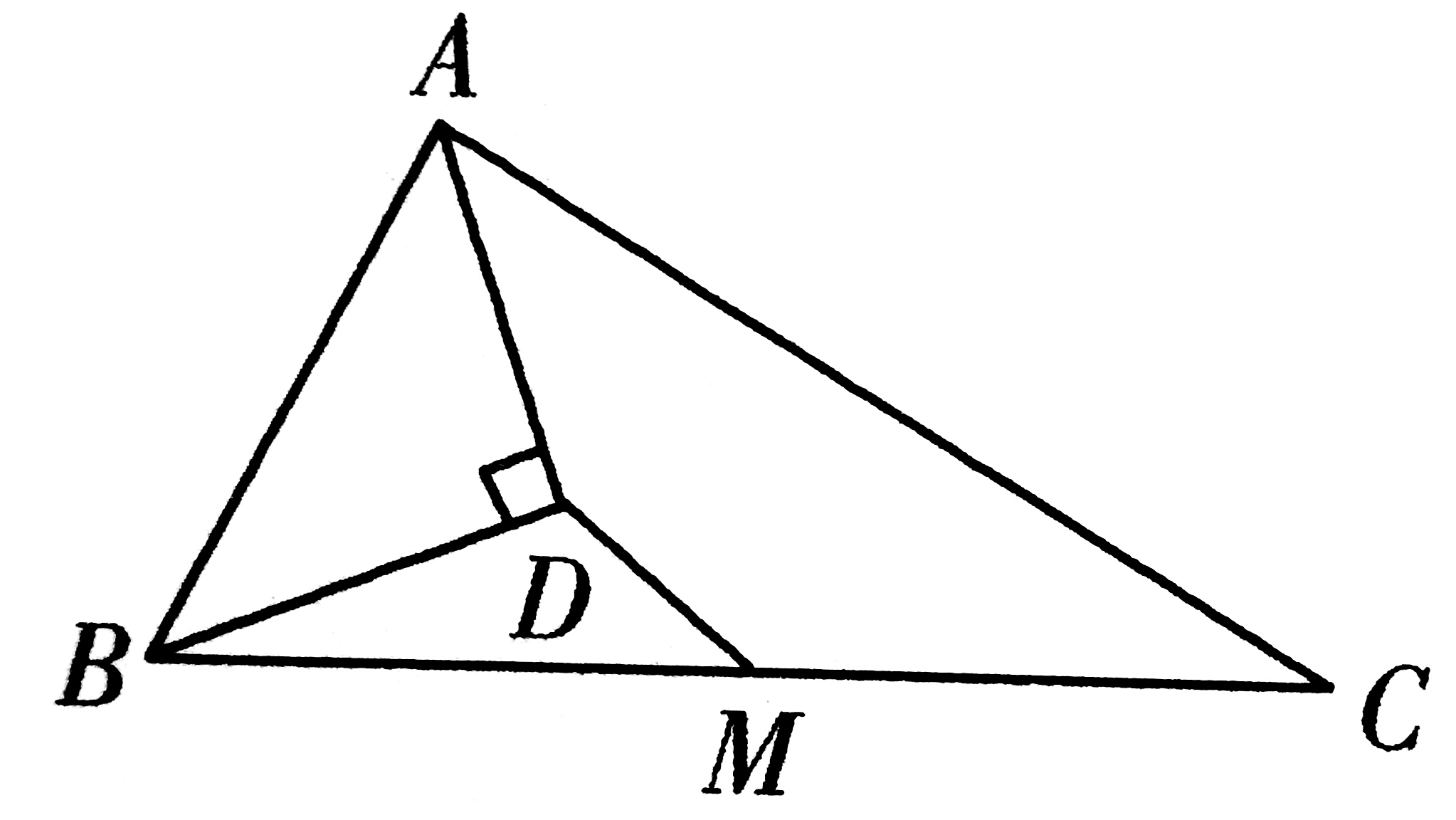
1、如图，在△ABC中，M为BC的中点，AD为∠BAC的角平分线，BD⊥AD于D。
     求证：(1)DM=1/2(AC—AB)
                 (2)判断∠ABD，∠DBM，∠C三个角之间关系，并加以证明。
                                                                                        
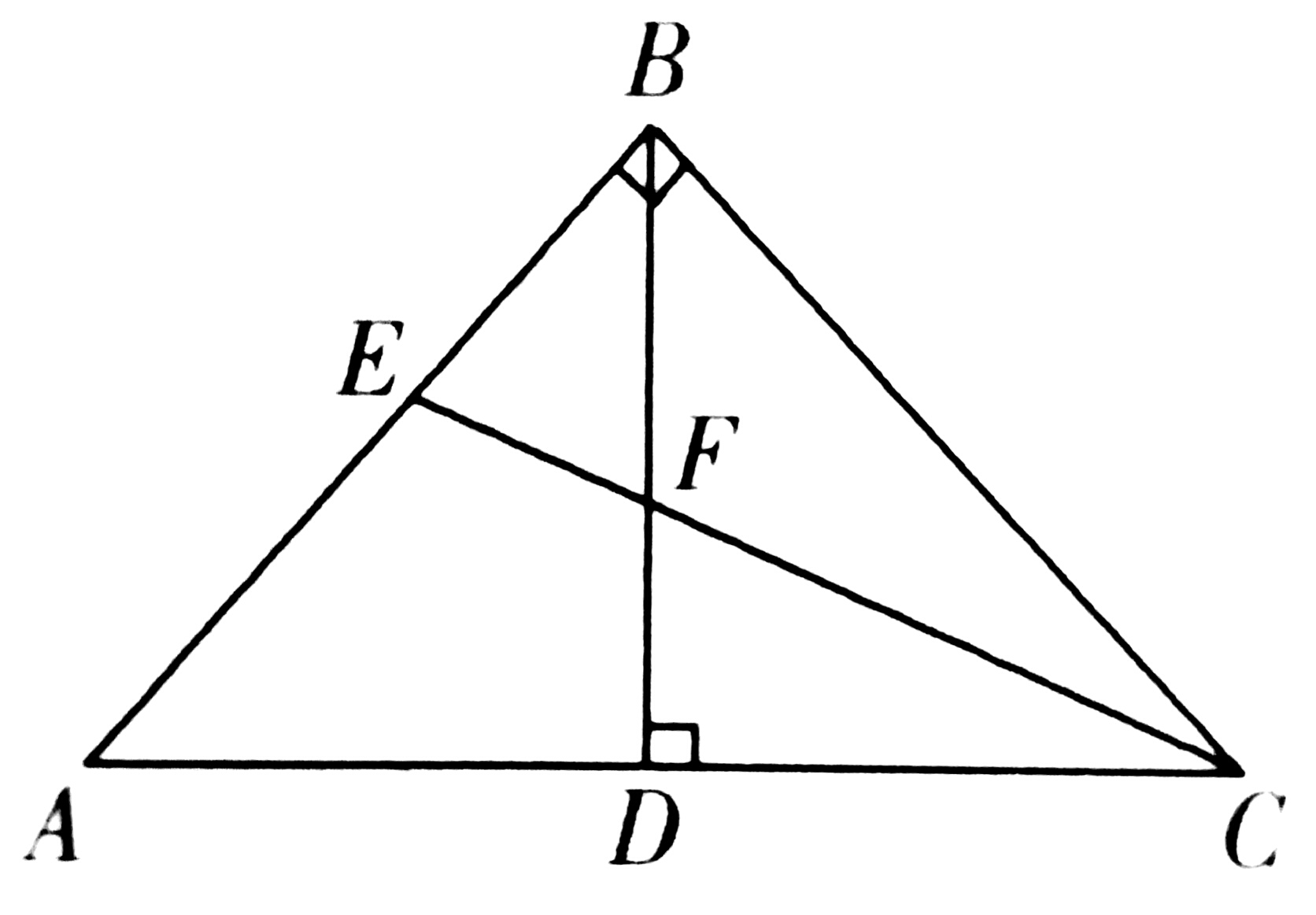
2、如图，在△ABC中，∠ABC=90°，AB=BC，BD⊥AC于点D，CE平分∠ACB并交AB于点E，交BD于点F。
      (1)求证：△BEF是等腰三角形
      (2)求证：BD=1/2(BC+BF)
                                                                                               
【参考答案】

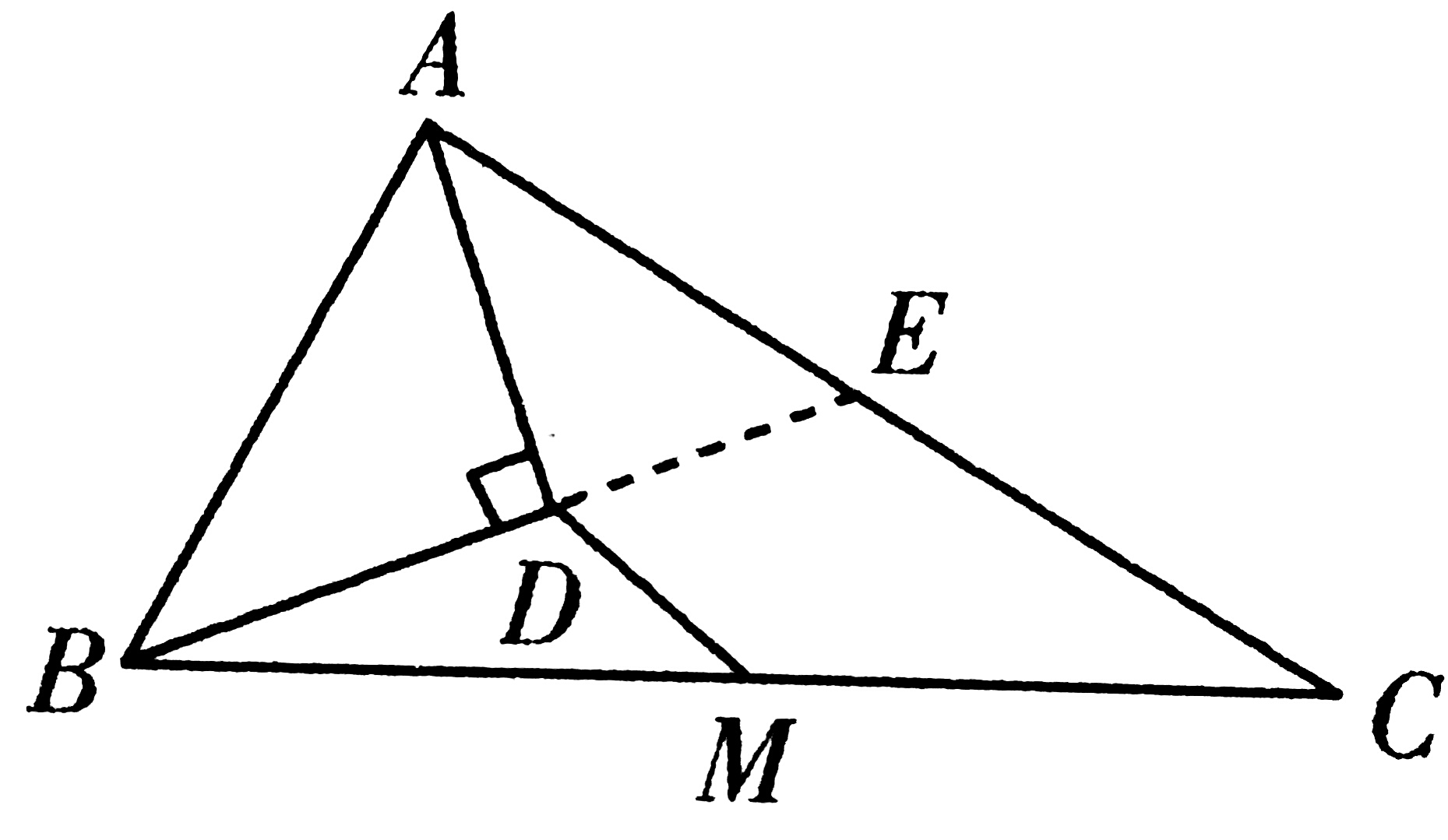
1、 (1) 作辅助线：延长BD至E
     ∵∠A左=∠A右
              AD=AD
         ∠D左=∠D右
     ∴△ABD≌△ADE(ASA)
     ∴AB=AE
         BD=DE
    又∵M为中点
        ∴DM=1/2EC
     又∵EC=AC—AB/AE
        ∴DM=1/2(AC—AB)

    (2) 判断结果：∠ABD=∠DBM+∠C

           ∵∠ABD=∠AED (三角形全等)
             ∠AED=∠DBM+∠C (三角形外角)
          ∴∠ABD=∠DBM+∠C (等量代换)
                                                                                             
2、(1)∵△ABC为等腰直角三角形  
         BD⊥AC
      ∴∠B左=∠B右=∠C=45°
      ∠C下=45÷2=22.5
    ∠F下=∠F上=90—22.5=67.5° (对顶角)
     ∴∠E=180—45—67.5=67.5°
      即∠E=∠F上
            BE=BF
  ∴△BEF是等腰三角形

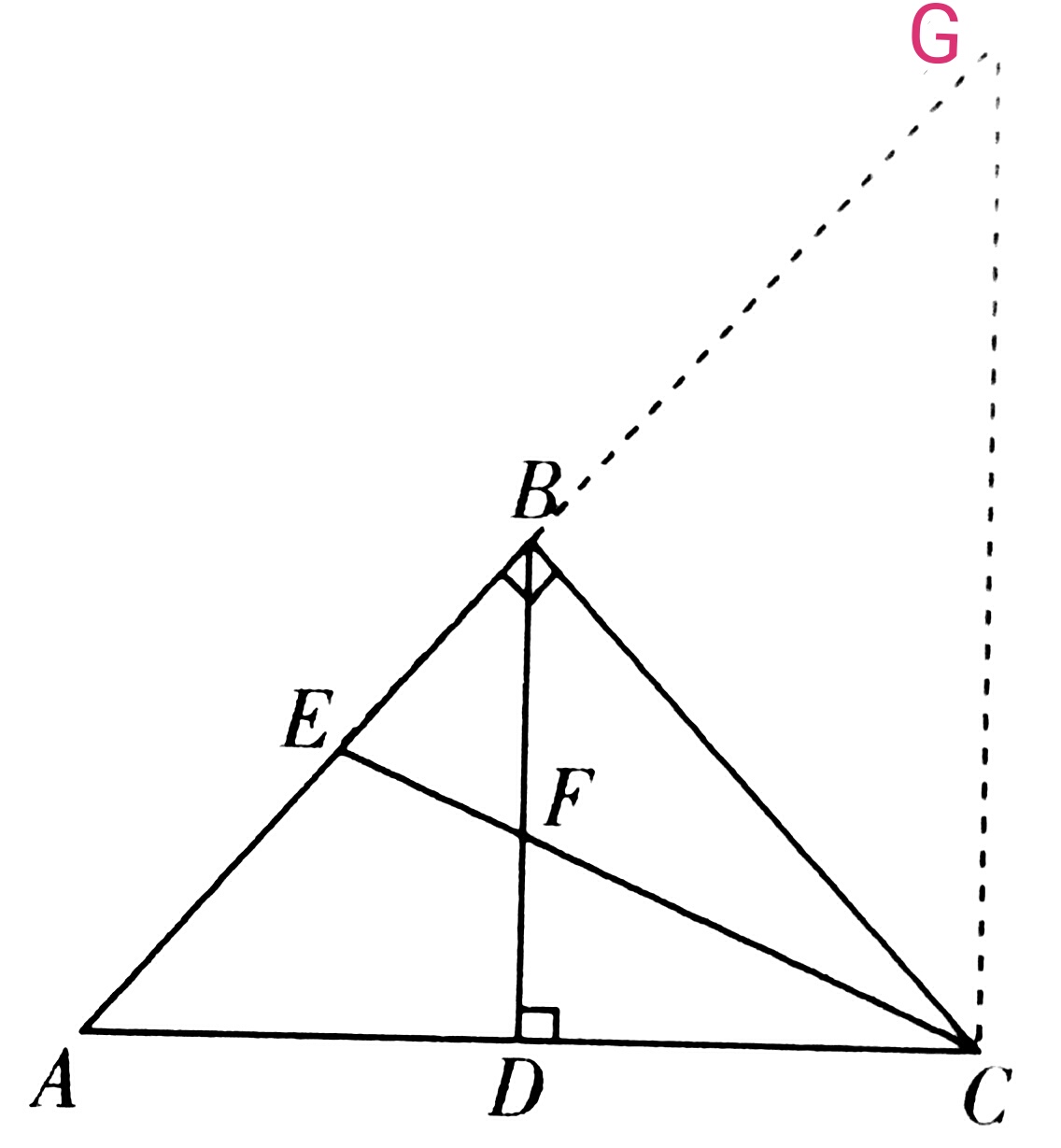
   (2)延长AB至G，BG=AB，连接CG
     ∵BG=BA DA=DC
     ∴BD=1/2GC (△ACG中，中位线)
     ∴∠F上=∠GCE (同位角)
   又∵∠F上=∠E上
       ∴∠GCE=∠E上
       ∴GC=GE (等腰三角形)
    又∵∠G=∠C右 (45°，△BCG中)
        ∴BG=BC
   最后：BD=1/2GC=1/2GE=1/2(BC+BF)
                                                                                                                             
苦心人，天不负。潜龙家教谭老师解题并录入，时间仓促错漏之处请您指正！