★如图，在△ABC中，BD、CE是△ABC的角平分线，BD, CE交于点O，过点O作OF⊥BC，垂足为F，若∠BAC =120°，OD·OE=12，BC—BE—CD=5，请您计算OF长度，谢谢！
                                                                                                       
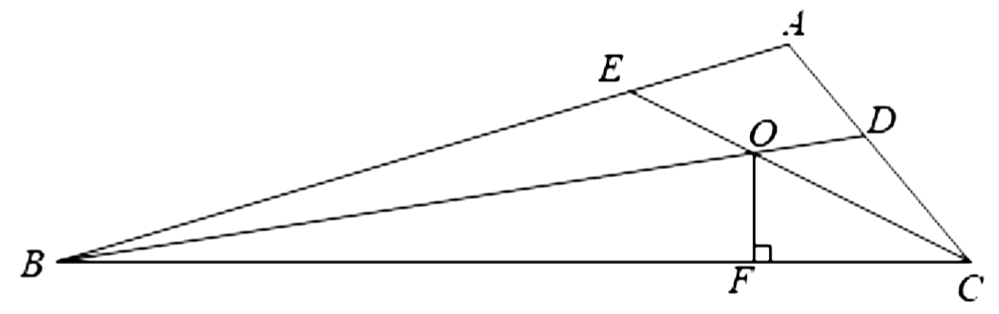
【题目解析】本题考查三角形角平分线，全等三角形，直角三角形面积算法。根据所给条件找出对应线段乘积，再推算出90度角∠GOH，然后根据三角形面积公式求出高OF是解题关键。

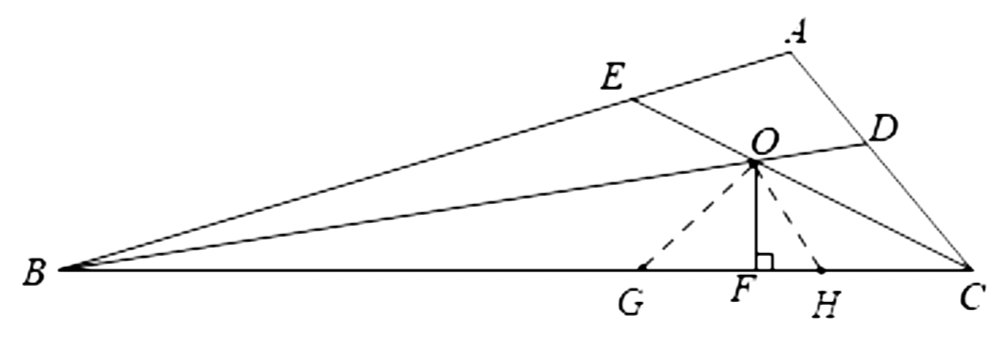
解：作辅助线：BC上取G、H，使BG=BE，CH=CD

∵△BOE≌△BOG  △COD≌△COH (SAS)
∴∠BOE=∠BOG  ∠DOC=∠HOC
∵∠BOE=∠DOC (对顶角)
∴以上四个角都相等
∵∠B下+∠C下=(180—∠A)÷2=30° (BD,CE是角平分线)
∴∠BOC=150°
∴∠BOE=180—150=30°
∠GOH=∠BOC—∠BOG—∠COH
            =150—30—30=90°
S△GOH=GO·HO÷2
而GO·HO=EO·DO 即=12
∴S△GOH=12÷2=6
而BC—BE—CD=GH=5
∴S△GOH=(GH·OF)÷2=6 (面积另一种算法)
    解得 OF=2.4
                                                                                                                                                  
一日之计在于晨，一生之计在于勤。潜龙家教谭老师解题并录入，感谢同学们光临！