★如图，直线AB：y₁=1/2x+m与x轴、y轴分别交于点A,B；直线CD：y₂=—2x+8与x轴、y轴分别交于点C,D；直线AB,CD相交于点E，且OD=2OA。
(1)请写出点A的坐标和m的值。
(2)请求出四边形OBEC面积。
(3)在坐标轴上是否存在点P，使得S△ABP=5/6S△BDE？若存在，写出所有满足条件的点P的坐标；若不存在，请说明理由。
    
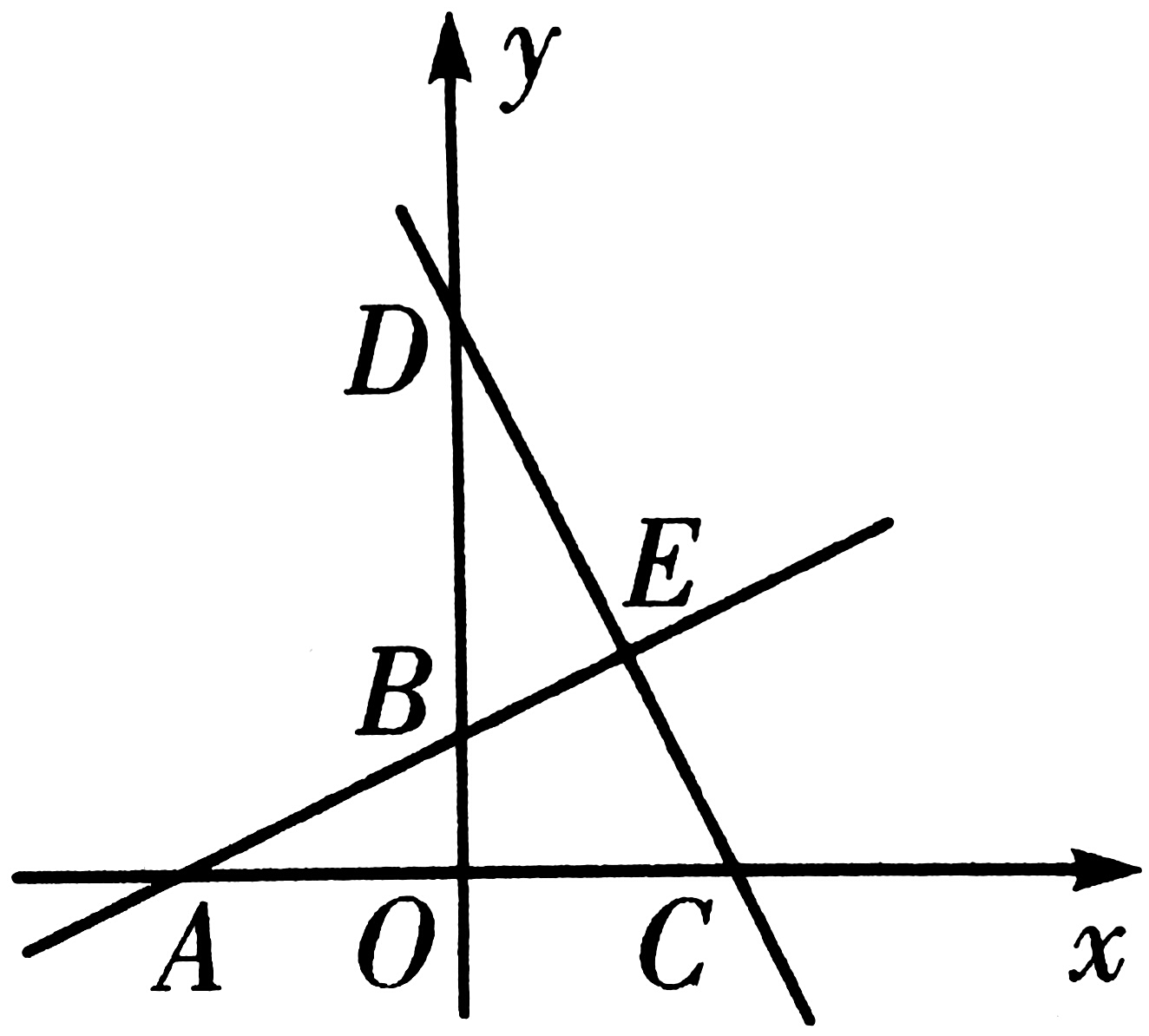
★解：(1)由直线CD：y₂=—2x+8，得
               D(0，8)，C(4，0)
             OD=8=2OA
            ∴OA=4
            A(—4，0)
      将A(—4，0)代入y₁=1/2x+m，得
          m=2

    (2) y₁=1/2x+2
        ∴B(0，2)
       y₁=1/2x+2
       y₂=—2x+8
     解得  x=12/5     y=16/5
  ∴E(12/5 ，16/5)
 四边形面积=△AEC面积—△ABO面积
  S△AEC=底·高÷2
               =(AO+OC)·16/5÷2
               =(4+4)·16/5÷2
               =64/5
 S△ABO=底·高÷2
               =AO·OB÷2
               =4·2÷2
               =4
     四边形面积： 64/5—4=44/5

(3) S△BDE=底·高÷2
                 =DB·E横÷2
                 =6·12/5÷2
                 =36/5
     ∴S△ABP=5/6·36/5=6
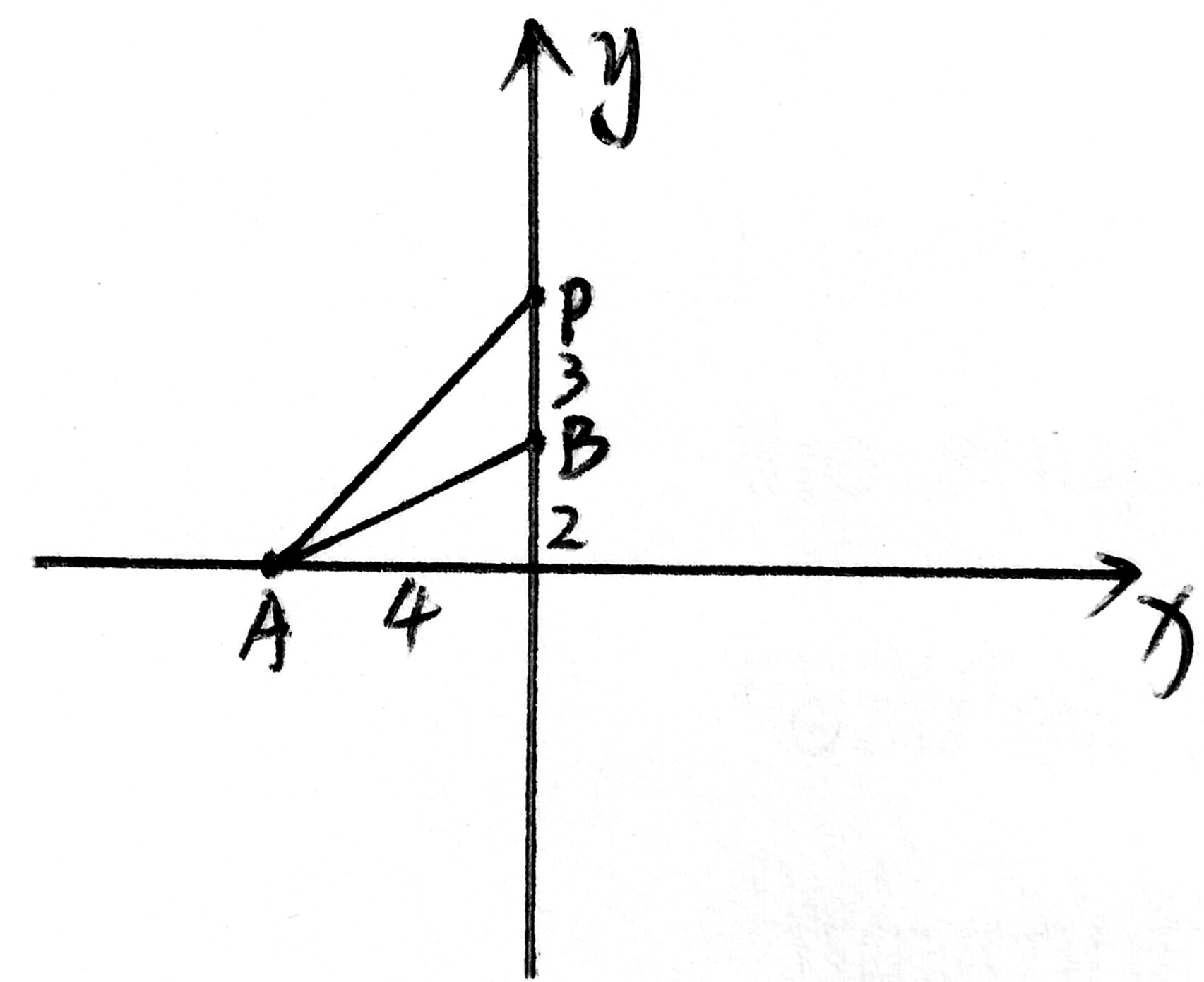
   ①P在y轴时，
       |P—2|·4÷2=6
        P=5 或—1
    ∴P(0，5)或(0，—1)
            
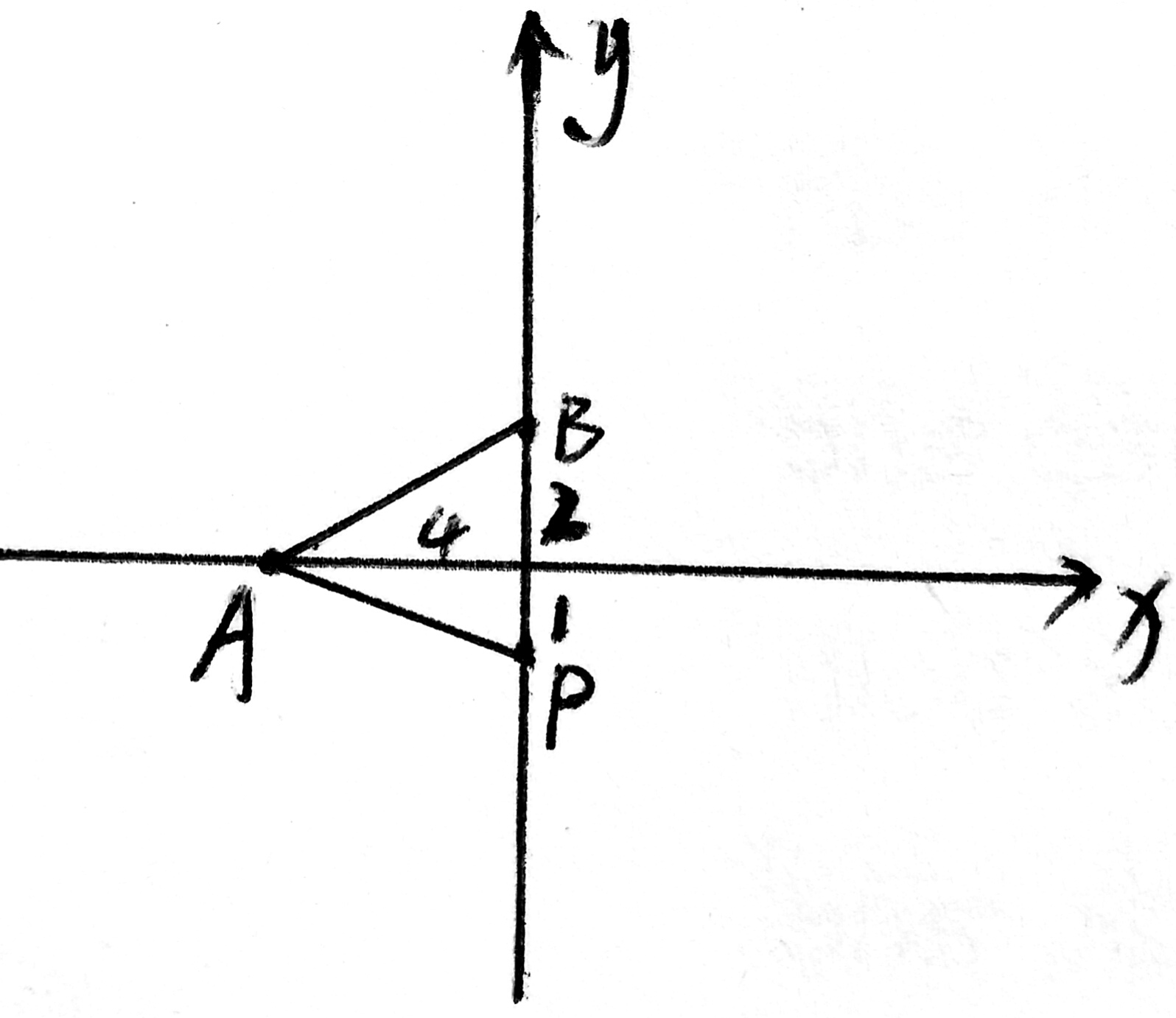
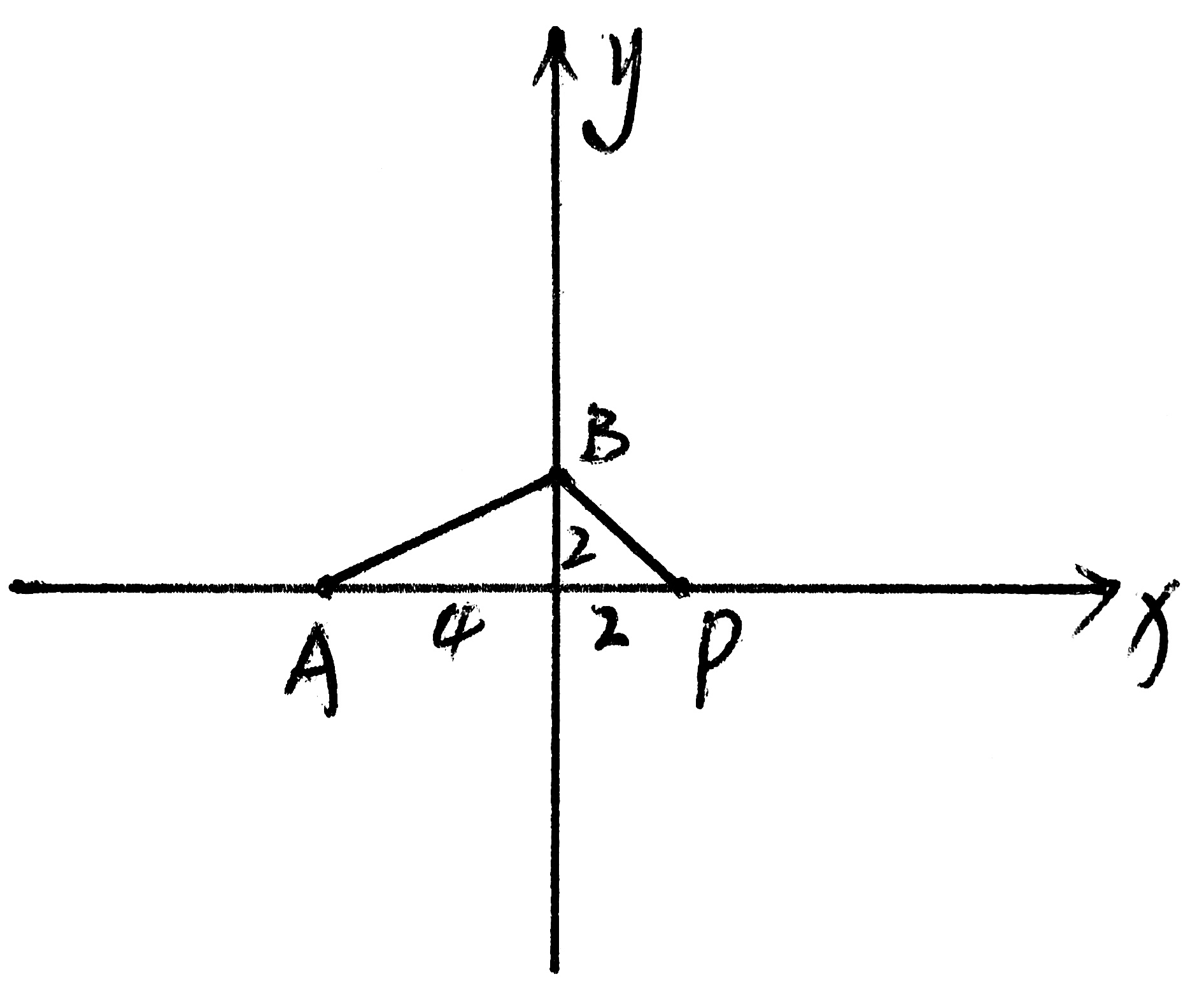
   ②P在x轴时，
      |P+4|·2÷2=6
        P=2 或—10
     ∴P(2，0) 或(—10，0)
            
综上①,② P(0，5) 或(0，—1)
                  P(2，0) 或(—10，0)

★以上由谭老师全程解题并录入，请同学们先自己动脑筋做一做，再核对答案，感谢！